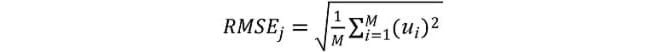- Published by:
- Department of Treasury and Finance
- Date:
- 1 May 2024
Ching Hin (Jeffrey) Wong and Nathan La1 2
1. Department of Treasury and Finance
2. The authors appreciate the participants at the 17th Western Economics Association International (WEAI) Conference for their valuable comments and suggestions.
Author contact details: veb@dtf.vic.gov.au.
Disclaimer: The views expressed are those of the author and do not necessarily reflect the views of the Victorian Department of Treasury and Finance.
Suggested Citation: Ching Hin (Jeffrey) Wong and Nathan La (2024), Applying machine learning in tax revenue forecasting. Victoria’s Economic Bulletin, May 2024, vol 8, no 2. DTF.
Abstract
Accurate revenue forecasting is essential for effective government budget planning. This study investigates whether the use of machine learning methods can enhance the accuracy of payroll tax and land transfer duty revenue forecasts in Victoria. We compare the performance of nine different forecasting methods, including traditional econometrics models and machine learning algorithms, based on various forecast horizons, loss functions and sample periods. We find that while machine learning methods do not improve payroll tax revenue prediction, they do marginally outperform simpler methods in forecasting land transfer duty. This study shows that machine learning methods are more effective for tax lines that have higher volatility and are more sensitive to economic fluctuations.
1. Introduction
Reliably forecasting revenue is crucial for government budget planning. However, revenue forecasting is a complex task, complicated by the interplay of economic fluctuations and government policies.
Consequently, economists have an interest in enhancing the precision of government revenue predictions. Contributing to this area, this study attempts to use machine learning to forecast tax revenue in Victoria, Australia.
The use of machine learning in time series forecasts can date back to Hu’s (1964) work on weather forecasting. With recent technological advancements, there has been a significant rise in the number of studies using machine learning, prompting us to examine its effectiveness in predicting government revenue. Machine learning has three primary advantages in forecasting. Firstly, it is effective in extracting useful signals from a large set of information. Secondly, it can uncover both linear and non‑linear relationships in the data. Thirdly, it is data-driven, which means it doesn’t require users to provide a model specification.
As some previous studies suggest that machine learning methods are effective in forecasting labour market movement (e.g. Gogas et al. 2022; Kreiner and Duca 2020)) and housing market movement (e.g. Milunovich 2020), our study focuses on the predictability of payroll tax and land transfer duty revenue, which are highly correlated with these two markets. We choose to focus on these taxes also because of their significant size. Our baseline results use quarterly taxation revenue data from the Victorian Department of Treasury and Finance (DTF), covering the period from June 1992 to December 2019. In some tests, we extend the sample period to September 2022 to cover the unusual time period during the COVID-19 pandemic.
Our study employs nine forecasting methods1, including autoregressive econometric models, regularized machine learning methods, ensemble machine learning methods, and the multilayer perceptron (MLP) neural network. In our baseline test, we include 23 features, including macroeconomic indicators provided by the Australian Bureau of Statistics (ABS) and Victorian property market indices provided by CoreLogic. We use a fixed window of the first 71 quarters of data to train our models and test forecast performance in the last 40 quarters of data (equivalent to 10 years). Consistent with common practice, we tune the hyperparameters of our machine learning models using K-fold cross-validation, with K set to 5.
Our main finding is that machine learning algorithms do not outperform simple autoregressive models for payroll tax forecasting, but might be useful in land transfer duty forecasting due to their ability the reduce data dimensionality and identify useful signals from a large set of features. More specifically, we find that of the models tested, an AR(4) model is the best performing model for payroll tax revenue forecasting, which implies that the autoregressive structure of payroll tax is the most important consideration for forecasting payroll tax.
Next, we find that Ridge Regression, which specialises in identifying useful signals from a large number of features, is the best method for land transfer duty forecasts, outperforming the benchmark AR(4) model with 25 per cent lower errors. However, this finding should be interpreted with caution, as the difference between the best machine learning method and the benchmarks is only marginally statistically significant at the 10 per cent level. Overall, the results suggest that the usefulness of machine learning methods is dependent on the characteristics of the tax line. The value of machine learning methods is higher when applied to tax lines that have higher volatility and more sensitive to fluctuations in economic conditions.
Furthermore, we conduct three additional tests to evaluate the performance of machine learning algorithms under difference scenarios. We focus on:
- examining whether machine learning algorithms demonstrate improved performance when incorporating property market conditions from various Australian cities in addition to Melbourne
- investigating the performance of machine learning algorithms under a data-rich environment, when the number of features increases to 166
- evaluating the performance of machine learning algorithms in forecasting during the COVID period with heightened uncertainty.
Our results suggest that including property market indices from other large cities and county-level macroeconomic statistics does not significantly improve machine learning algorithm performance. In fact, increasing the feature set’s dimensionality can lead to a decrease in algorithm performance, as it becomes harder for the algorithms to extract valuable information.
On the other hand, during the COVID-19 pandemic period’s extreme observations we find that machine learning algorithms can be valuable. Interestingly, their usefulness takes on a different aspect as compared to the baseline results. In our baseline results, regularized machine learning methods that focus on signal identification prove beneficial during normal periods. During abnormal periods like the COVID-19 crisis, machine learning models that explore the non‑linear relationship between the target variable and features, such as tree-based methods and neural network, perform better.
In summary, our study contributes to the literature comparing simple and sophisticated methods in forecasting fiscal variables (e.g. Feenberg et al. 1989; Gentry 1989; Favero and Marcellino 2005; Carriero, Mumtax, and Theophilopoulou 2015). Our finding is consistent with a recent study (Chung, Williams, and Do, 2022), which shows that machine learning is not helpful in forecasting most types of government revenue in the United States, except for land transfer duty. Furthermore, we also contribute to the emerging literature on the use of machine learning approaches in economic forecasts (e.g. Gu, Kelly, and Xiu, 2020; Medeiros, Vasconcelos, Veiga, and Zilberman, 2021; Babii, Ghysels, and Striaukas, 2022; Milunovich, 2020).
The rest of the paper is organized as follows. Section 2 discusses the background of revenue forecasting and the taxation structure in Victoria. Section 3 outlines the forecasting methods covered in this study. Section 4 discusses the detailed setting of this study. Section 5 presents the main baseline results and Section 6 shows additional scenario analyses. Section 7 concludes.
Footnotes
[1] The forecasting models covered in this paper may not necessarily reflect the actual models used by the DTF in its official revenue forecasting process.
2. Background
Background information for this research article.
2.1 Common approaches for revenue forecasting
Revenue forecasts provide critical context to governments to inform their decision-making on budgeting and revenue policy. However, whether we should use simple or sophisticated methods remains an outstanding question. Favero and Marcellino (2005) conducted a comprehensive comparison of different forecasting methods used by governments to predict fiscal variables, including univariate autoregressive and moving average models, vector autoregressions (VARs), and small-scale semi-structural models. They find that simple univariate time series methods tend to provide effective and unbiased forecasts, outperforming multivariate models that rely on a system of macroeconomic variables. They attribute this to the difficulty of modelling the joint behaviour of multiple macroeconomic variables in a short sample with significant institutional and economic changes, as well as the robustness of simple methods in accounting for structural breaks.
Conversely, some more recent studies show that multivariate models can improve forecast accuracy. These studies usually utilise longer sample periods and more advanced forecasting techniques, compared to Favero and Marcellino (2005). For instance, Carriero, Mumtax, and Theophilopoulou (2015) present evidence that their Bayesian Vector Autoregressions (BVARs) are more effective than simple forecast approaches, as they can better summarise the information contained in a large dataset and allow for time variation in the coefficients. The authors demonstrate that BVARs outperform simple models in both point and density forecasting using data from the United States and Europe. In our study, we add to this ongoing discussion regarding the relative performance of different revenue forecasting techniques by incorporating machine learning models to predict taxation revenue in Australia.
Machine learning methods have been used for forecasting as early as Hu’s (1964) work on weather forecasting. With technological advancements, there has been a substantial increase in the number of studies utilising machine learning for time series forecasting. However, evidence of the effectiveness of these algorithms remains inconclusive. On one hand, some recent studies show that machine learning methods can outperform traditional methods in forecasting stock market returns (Gu, Kelly, and Xiu 2020), predicting inflation (Medeiros, Vasconcelos, Veiga, and Zilberman 2021), and nowcasting GDP growth (Babii, Ghysels, and Striaukas 2022). On the other hand, other studies suggest that machine learning algorithms do not outperform simple models such as ARIMA (Makridakis, Spiliotis, and Assimakopoulous 2018) and some are not even better than random walks (De Gooijer and Hyndman 2006). Thus, our paper is a case study that also contributes to the emerging literature on the effectiveness of machine learning algorithms in time series forecasting.
2.2 Taxation revenue in Victoria
The Victorian Government collects revenue from a range of taxes, including payroll tax, land transfer duty, land tax, gambling taxes, motor vehicle taxes, and insurance taxes.1 Taxation revenue is utilised to fund public services and infrastructure. Every year, Budget Paper No. 5 Statement of Finances contains the Estimated Financial Statements and accompanying explanatory notes that set out the forecast financial results for the Victorian general government sector for the next four years.
This study will focus on forecasting the two biggest tax lines of the state, namely payroll tax and land transfer duty. Victoria imposes payroll tax on employers when the total taxable wages exceed a specific threshold.2 Land transfer duty, on the other hand, is one-time tax levied on most real estate transactions and is calculated based on dutiable value of the property.3 In addition to their importance, we are focusing on these two taxes because they are closely tied to the employment and housing markets, and previous research suggests that machine learning methods can effectively predict their trends (e.g. Gogas et al. 2022; Kreiner and Duca 2020; Milunovich 2020).
It is worth noting that forecasting land transfer duty and forecasting payroll tax present different issues. As discussed in DTF’s 2023 submission to the Victorian Parliamentary Inquiry on land transfer duty fees, forecasting land transfer duty is typically considered a more challenging task (DTF, 2023):
'Revenue forecasts provide critical context to governments to inform their decision-making on budgeting and revenue policy. While having accurate forecasts for all revenue sources is important, land transfer duty typically contributes around 9 per cent of total general government sector revenue each year, and its cyclical volatility can disproportionately affect overall revenue forecast errors when compared to most other sources of taxation revenue.'
2.3 Land transfer duty and payroll tax revenue from 1990 to 2022
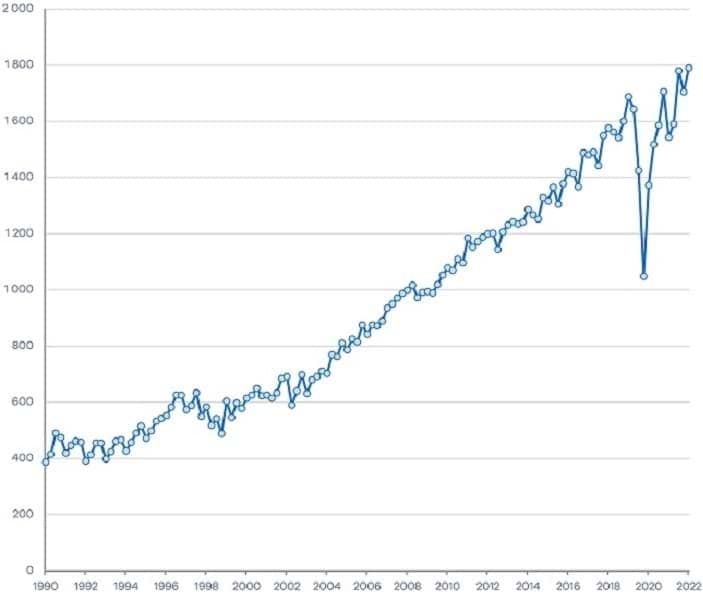
Figures 1a and 1b show the quarterly payroll tax and land transfer duty revenue (seasonally adjusted) from 1990 to 2022. We can see that while both series show an upward trend, land transfer duty revenue is much more volatile than payroll tax revenue. This aligns with our expectation, as land transfer duty is influenced by movements in the housing market, which is typically more volatile than the labour market that affects payroll tax revenue. In YR2021-22, payroll tax and land transfer duty generated around $1.7 billion and $2.6 billion for the Victorian Government per quarter, respectively.
We can also see the significant shifts in the patterns of payroll tax revenue and land transfer duty revenue since 2020. Specifically, payroll tax revenue experienced a steep decline at the onset of the COVID-19 pandemic due to the weakened labour market and government payroll tax relief policies, while land transfer duty revenue has seen a substantial increase since late 2020, in correlation with the robust growth in property prices.
Figure 1a. Payroll tax from 1990-2022
Figure 1b. Land transfer duty from 1990-2022
Footnotes
[1] In 2022-23, the total taxation revenue of the Victorian Government was about $32.4 billion. View the 2022-23 Financial Report.
[2] For more information on payroll tax, visit the State Revenue Office website.
[3] For more information on land transfer duty, visit the State Revenue Office website.
3. An overview of forecasting algorithms
An overview of the two benchmarks employed in this study and machine learning methods.
3.1 Benchmarks
We employ two benchmarks in this study, including a simple forecast based on the historical average during the training period (a random walk with drift) and an AR (4) model. We choose these two benchmarks primarily because they are easy to implement and often serve as the starting point for time series analyses. Also, Favero and Marcellino (2005) show that simple approaches may be just as effective, if not superior, to complex models for forecasting fiscal variables, especially for short-term horizons and when the sample size is relatively small.
3.2.1 Regularization methods
LASSO, Ridge Regression, and Elastic Net
Regularization methods are techniques that aim to reduce the dimensionality of data and mitigate the risk of overfitting in a model. In time series forecasting, they are typically employed to extract valuable signals from a large set of potential predictors. LASSO (Tibshirani, 1996) and Ridge Regression (Hoerl and Kennard, 1970) are two different techniques used for regularization. Both methods work by adding a penalty term to the cost function of the linear regression model, which restricts the size of the coefficients and compels the model to be less complex.
The major difference between LASSO and Ridge Regression is the type of penalty used to shrink the regression coefficients. While LASSO’s penalty term forces some coefficients to be exactly zero, resulting in a model that selects only a subset of most important features for predicting the target variables, the Ridge Regression method only shrinks the magnitude of all coefficients toward zero, but not exactly zero. The penalty terms of LASSO and Ridge Regression are also referred as the L1 penalty and L2 penalty, respectively.
Another regularization method covered in this study is the Elastic Net (Zou and Hastie, 2005), which was developed with the aim of overcoming the limitations of LASSO and Ridge Regression. Similar to LASSO and Ridge Regression, Elastic Net adds a penalty term to the objective function of a linear regression model. The Elastic Net penalty term combines L1 and L2 regularization, enabling it to strike a balance between the feature selection capabilities of LASSO and the stability of Ridge Regression.
3.2.2 Ensemble methods
Ensemble machine learning methods are commonly used in forecasting. These methods combine multiple models to improve accuracy. The basic idea behind them is to leverage the strengths of different models and minimise their weaknesses. The ensemble methods covered in this study include Random Forest, Gradient Boosting, and Extreme Gradient Boosting (XGBoost).
Random forest
The core element of the random forest method (Breiman, 2001) is the decision tree learning method. Decision trees are used to build the prediction models from specific datasets, in which data is split into subsets recursively based on a set of rules. The resulting tree structure consists of connected nodes representing decision points. Random forest is a combination of multiple decision trees. It creates multiple decision trees by sampling the data and features with replacement, leading to multiple sub‑samples of the original data. These sub-samples are used to train individual decision trees that are eventually combined to produce the final forecast.
Gradient Boosting
Gradient boosting (Friedman, 2001) is also a tree-based method. Unlike the random forest method which has independent trees, each tree in gradient boosting is made conditional on previous trees. More specifically, gradient boosting aims to minimise the difference between the predicted and actual values of the target variable (a loss function) by iteratively adding decision trees to the model. At each iteration, the decision tree is trained on the errors of the previous tree, which allows the model to focus on the areas where it performed poorly in the previous iteration.
Extreme Gradient Boosting
Extreme Gradient Boosting (XGBoost) is a variant of gradient boosting that includes additional features and techniques to improve performance, such as regularization of the objective function, early stopping and subsampling. These features help to control overfitting and improve the accuracy and speed of the model (Chen and Guestrin, 2016). XGBoost is also often less sensitive to the choice of hyperparameters, which makes it easier to turn the model.
3.2.3 Neural network
Multilayer perceptron
Multilayer perceptron (MLP) is a type of artificial neural network that consists of multiple layers of interconnected nodes (neurons). The MLP is a feedforward neural network, which means that information flows in only one direction, from the input layer, through the hidden layers, to the output layer. The key feature of MLP is its ability to learn complex non‑linear relationships between the input and output variables (Rosenblatt, 1961; Rumelhart, Hinton, and Williams, 1985).
4. The forecasting exercise
Information about the design of the study and forecast evaluation.
4.1 Design of the study
This forecasting exercise is performed in pseudo real time, which means that we never use information that is not available at the time the forecast is made but do use final vintage data. We use quarterly taxation revenue from DTF. Our baseline analysis spans from June 1992 to December 2019, which amounts 111 quarterly observations. Our target variables are the growth rates (log-difference) of payroll tax and land transfer duty revenue. In our baseline results, we use a total of 23 economic variables. These variables include property market price and sales indices provided by CoreLogic as well as macroeconomic and labour market statistics provided by the ABS. In later tests, we increase the number of features to 166 in order to assess the performance of machine learning algorithms within a data-rich environment.
This study uses a fixed estimation window method. Except for the random walk model, we employ four-quarter lagged information in other algorithms to conduct forecasting. We train our models using the first 71 observations and test the out-of-sample forecast performance in the last 40 observations (equivalent to 10 years). The hyperparameters of our machine learning methods are tuned using the K-fold cross validation method. The basic idea behind K-fold cross validation is to split the available data into K subsets of folds, then the model is trained and tested K times, with a different fold held out as the validation set each time. The biggest advantage of using K-fold cross‑validation is that it provides a more accurate estimate of the model’s performance than a single validation set, especially when the data size is small. Following common practices, we set K to be 5.
4.2 Forecast evaluation
Evaluations of predictive accuracy are conducted on the basis of computed errors for forecast horizons h = 1, 2, 3, 4 for algorithm j = 1, 2,…, 9. We perform forecast evaluations on the basis of two measures: (i) relative root mean squared errors (RMSE) and (ii) the Diebold and Mariano (DM) test.1
The root mean squared errors are computed for each algorithm and horizon as follows:
where ui
Footnotes
[1] DM test was proposed by Diebold and Mariano (1995) to statistically compare the predictive accuracy of two competing forecasting models. The basic idea is to test whether the forecast errors of the competing forecasting models is statistically different. The null hypothesis of the test is that the two models have the same forecasting accuracy, while the alternative hypothesis is that the forecast errors of one is significantly smaller than the other, implying superior performance.
5. Main analyses
Information on the baseline results, and where the predictability of land transfer duty revenue comes from.
5.1 Baseline results
The performance of our forecast algorithms is summarized in Table 1 based on the relative RMSE with the random walk with drift model used as the benchmark. Firstly, for payroll tax forecasting, we find that of the models tested, AR(4) is the best across all forecast horizons, outperforming the benchmark with about a 25 per cent lower RMSE. Elastic Net is the most effective machine learning model, with an RMSE slightly higher than that of AR(4). The result implies that the autoregressive structure is the most important consideration when forecasting payroll tax revenue. Machine learning methods that explore information from the selected features are not very useful in further improving forecast accuracy. This finding is consistent with the stability of payroll tax revenue observed in Figure 1a, which implies that payroll tax revenue is less sensitive to economic fluctuations.
Turning to the prediction of land transfer duty, we observe that the random walk with drift model and the autoregressive model yield similar results. This suggests that autocorrelation in land transfer duty is not particularly useful, in contrast to payroll tax forecasting. The best-performing machine learning model, LASSO, achieves approximately a 20 per cent lower RMSE1 compared to the random walk and autoregressive models. This indicates that machine learning can enhance the accuracy of land transfer duty revenue forecasts. More specifically, regularized machine learning algorithms that are designed to reduce data dimensionality and extract useful signals from a large set of information prove particularly useful. However, it is crucial to interpret these findings with caution, as even the best performing machine learning model only marginally outperform the random walk benchmark at the 10 per cent significance level under the DM test.
Overall, our findings suggest that the efficiency of machine learning methods is associated with the nature of the tax line. Machine learning methods may not provide additional value for stable tax lines, but they can be more useful when applied to tax lines that are highly sensitive to economic fluctuations.
Table 1. Forecast performance
This table shows the performance (measured by RMSE) of 10 different methods in forecasting one- to four-step ahead payroll tax and land transfer duty revenue in Victoria.
| Payroll | Land transfer duty | |||||||
|---|---|---|---|---|---|---|---|---|
| Forest horizon | t+1 | t+2 | t+3 | t+4 | t+1 | t+2 | t+3 | t+4 |
| Random walk with drift | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| AR(4) | 0.75 | 0.67 | 0.73 | 0.99 | 1.02 | 1.07 | 1.03 | 1.08 |
| Ridge Regression | 1.60 | 1.50 | 1.45 | 2.12 | 1.22 | 1.34 | 1.17 | 1.28 |
| LASSO | 0.89 | 0.81 | 0.88 | 1.34 | 0.88 | 0.76 | 0.77 | 0.84 |
| Elastic Net | 0.95 | 0.75 | 0.86 | 1.25 | 0.88 | 0.75 | 0.76 | 0.85 |
| Gradient Boosting | 1.11 | 1.07 | 1.22 | 1.98 | 1.11 | 1.10 | 1.20 | 1.21 |
| XGBoost | 1.28 | 1.29 | 1.76 | 2.50 | 0.91 | 0.82 | 0.85 | 0.82 |
| Random Forests | 1.13 | 1.10 | 1.28 | 2.11 | 0.91 | 0.84 | 0.89 | 0.90 |
| MLP | 1.02 | 0.99 | 0.98 | 1.12 | 1.02 | 1.11 | 1.02 | 0.93 |
5.2 Where does the predictability of land transfer duty revenue come from?
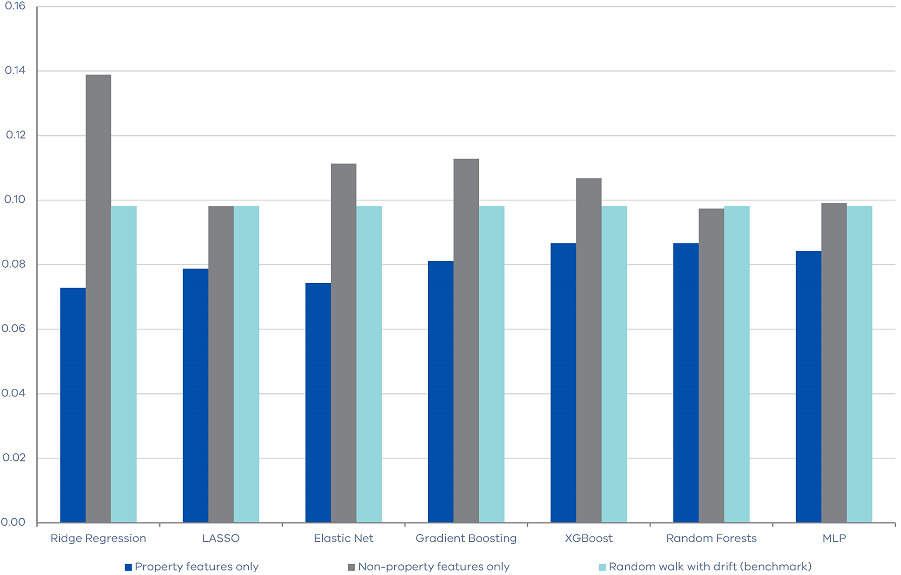
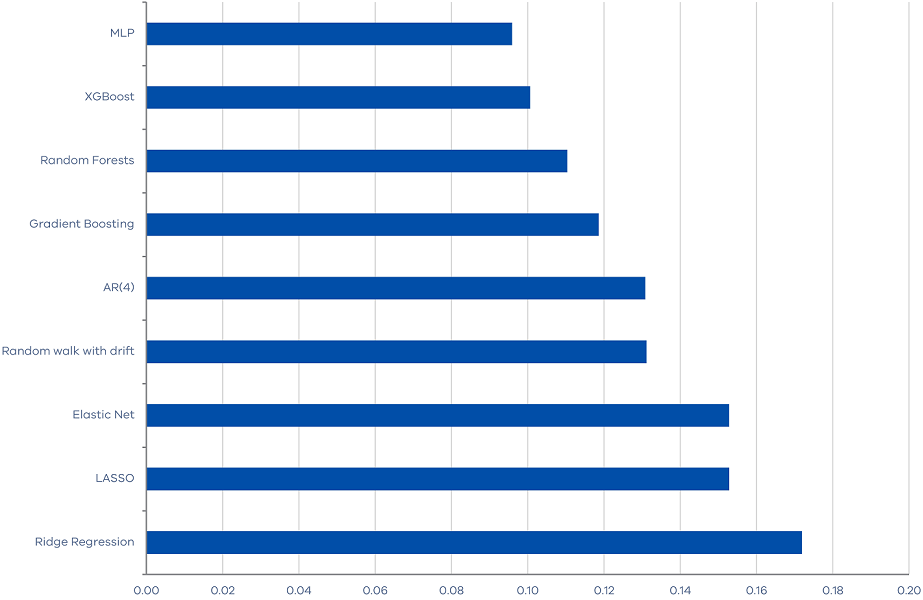
As mentioned above, our features contain property market indices from CoreLogic as well as macroeconomic indicators from the ABS. In this sub-section, we disentangle what drives the predictability of land transfer duty revenue. More specifically, we separately run the algorithms with property features only and non-property features only, then we compare them alongside with the random walk with drift method as the benchmark. This exercise focuses on one-quarter ahead forecast.
Unsurprisingly, Figure 1 shows that the property features are the more important features for land transfer duty forecasting. For example, the RMSE of Ridge Regression is 0.07 when using property features, but 0.14 when using non‑properties features. It is interesting to note that when property features are excluded, machine learning models do not outperform the simple benchmark, implying that historical macroeconomic indicators might have limited predictive power on future land transfer duty revenue. Our results also imply that machine learning algorithms are effective in identifying useful signals (i.e. property market features) from a large set of features, which might contain less useful information (i.e. macroeconomic features).
Figure 2. RMSEs of machine learning algorithms using property and non-property features
Footnotes
[1] In unreported tests, we find that our results remain robust when using the Mean Absolute Error (MAE) as the loss function.
6. Additional analyses
Additional analyses, and going deeper into assessing their performance enhancement in specific scenarios.
In this section, after discovering that machine learning techniques can be useful in forecasting land transfer duty revenue, we go deeper into assessing their performance enhancement in specific scenarios. We explore three primary directions, with a focus on:
- examining whether machine learning algorithms demonstrate improved performance when incorporating property market indices from various Australian cities in addition to Melbourne
- investigating the performance of machine learning algorithms within a data-rich environment comprising 166 features
- evaluating the performance of machine learning algorithms in forecasting during the COVID period with heightened uncertainty.
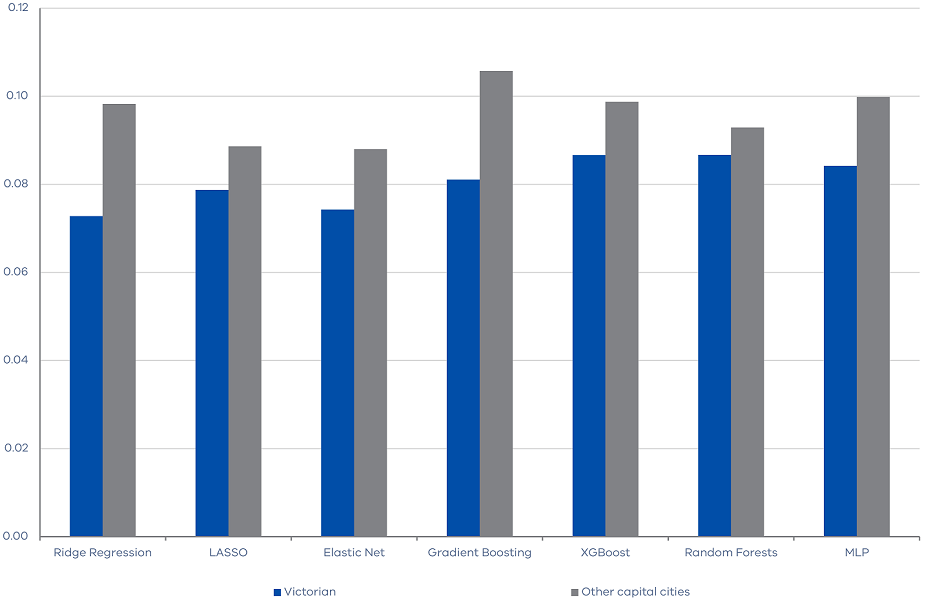
6.1 Do market conditions of other Australian large cities forecast Victorian land transfer duty?
We start by investigating whether the housing market indices of other Australian large cities provide any information about the future movements of Victorian land transfer duty revenue. In particular, we include the CoreLogic housing indices for Sydney, Perth, Brisbane, and Hobart in the machine learning algorithms. Figure 3 shows that including housing market indices of other large cities does not reduce the RMSEs, suggesting that they do not provide too much additional information on the future movement of Victorian land transfer duty revenue.
Figure 3. RMSE of machine learning algorithms with other cities property features
6.2 Performance of machine learning algorithms within a data-rich environment
Subsequently, we expand our feature set by incorporating country-level macroeconomic variables into the original 23 features, resulting in a total of 166 features. This attempt serves two distinct purposes. First, it assesses the relevance of country-level macroeconomic conditions in the forecast of Victorian land transfer duty revenue. Moreover, it also evaluates the performance of machine learning techniques within a data-rich environment. The outcomes shown in Figure 4 indicate that the inclusion of country-level features does not lead to a reduction in forecast errors. In fact, with the expansion of the information pool, our algorithms encounter increased difficulty in discerning valuable insights, which subsequently results in slightly heightened forecasting errors in most algorithms.
Figure 4. RMSE of machine learning algorithms within a data-rich environment
6.3 Performance of machine learning algorithms during COVID
The final additional test is to evaluate the performance of machine learning algorithms during the high uncertainty period of the COVID-19 pandemic, from March 2020 to September 2022. Since this period spans only nine quarters and includes some highly extreme observations, we will simply compare the Mean Absolute Errors (MAEs) of our forecasting algorithms without commenting on the statistical significance. Also, we only include property market features which are proven the most relevant. Our results demonstrate that some machine learning methods perform quite well. In particular, the MLP neural network outperform the benchmark random walk and autoregressive models with less than 30 per cent forecast errors.
Moreover, it is interesting to note that the machine learning methods that perform well differ from those that perform well in the baseline results. In the baseline results, regularization methods perform best, implying that the strong performance of machine learning algorithms stems from their ability to reduce data dimensionality and extract useful information from a large set of features. But, these methods, such as Elastic Net, LASSO, and Ridge Regressions, are the worst performing models during the COVID-19 period when there is substantial noise in the features. Conversely, ensemble methods and neural network, such as MLP and XGBoost, which explore the non‑linear relationship between the target variable and the features, tend to perform well during the COVID-19 period.
Figure 5. MAE of machine learning algorithms for the period from March 2020 to September 2022
7. Conclusion
Conclusion for this Victoria’s Economic Bulletin research article.
This paper documents our attempt to apply machine learning techniques to predict payroll tax and land transfer duty revenue in Victoria. We compare the effectiveness of these techniques against simpler econometric models by utilising different loss functions, forecast horizons, and sample periods.
Our findings suggest that machine learning methods do not outperform simpler models for payroll tax forecasting but might be useful for land transfer duty forecasting.
This conclusion aligns with a recent study by Chung, Williams and Do (2022), which shows no significant improvement when using machine learning to forecast government revenue in the United States, except for the prediction of land transfer duty revenue.
Overall, our findings indicate that simple methods can be equally effective as advanced approaches when forecasting tax lines that are more stable, whereas sophisticated methods may offer added benefits when dealing with a more volatile tax line.
8. References
References for this Victoria’s Economic Bulletin research article.
Babii A, Ghysels E and Striaukas J (2022) ‘Machine learning time series regressions with an application to nowcasting’, Journal of Business and Economic Statistics, 40, 1094–1106.
Breiman L (2001) ‘Random forests’, Machine learning 45, 5-32.
Carriero A., Mumtaz H. and Theophilopoulou A (2015) ‘Macroeconomic information, structural change, and the prediction of fiscal aggregates’, International Journal of Forecasting, 31(2): 325-348.
Chen T and Carlos G (2016) ‘Xgboost: A scalable tree boosting system.’
Chung IH, Williams DW and Do MR (2022) ‘For Better or Worse? Revenue Forecasting with Machine Learning Approaches’, Public Performance & Management Review, 45(5): 1133-1154.
De Gooijer JG and Hyndman RJ (2006) ‘25 years of time series forecasting’, International journal of forecasting, 22(3): 443-473.
Department of Treasury and Finance (2023), ‘Submission to Victorian Parliamentary Inquiry on Land Transfer Duty Fees’
Duncan G, Gorr W and Szczypula J (1993) ‘Bayesian forecasting for seemingly unrelated time series: Application to local government revenue forecasting’, Management Science 39: 275–293.
Favero CA., Marcellino M and Neglia F (2005) ‘Principal components at work: the empirical analysis of monetary policy with large data sets’, Journal of Applied Econometrics 20, No. 5, 603-620.
Feenberg DR., Gentry WM, Gilroy D and Rosen HS (1989) ‘Testing the rationality of state revenue forecasts’, The Review of Economics and Statistics.
Friedman JH (2001) ‘Greedy function approximation: a gradient boosting machine’, Annals of statistics, 1189-1232.
Gentry W M (1989) ‘Do state revenue forecasters utilize available information?’, National Tax Journal 42: 429–439.
Gogas P, Papadimitriou T and Sofianos E (2022) ‘Forecasting unemployment in the euro area with machine learning’, Journal of Forecasting, 41(3): 551-566.
Gu S, Kelly B and Xiu D (2020) ‘Empirical asset pricing via machine learning’, Review of Financial Studies 33: 2223–2273.
Hoerl AE and Robert WK (1970) ‘Ridge regression: Biased estimation for nonorthogonal problems’, Technometrics 12.1: 55-67.
Kreiner A. and Duca J (2020) ‘Can machine learning on economic data better forecast the unemployment rate?’, Applied Economics Letters, 27(17): 1434-1437.
Makridakis S., Spiliotis E and Assimakopoulos V (2018) ‘Statistical and Machine Learning forecasting methods: Concerns and ways forward’, PLOS ONE, 13(3): e0194889.
Medeiros MC, Vasconcelos, Veiga A and Zilberman E (2021) ‘Forecasting inflation in a data-rich environment: The benefits of machine learning methods’, Journal of Business and Economic Statistics 39: 98–119.
Milunovich G (2020) ‘Forecasting Australia’s real house price index: A comparison of time series and machine learning methods’, Journal of Forecasting, 39(7): 1098-1118.
Rosenblatt F (1962) ’Principles of neurodynamics: Perceptrons and the theory of brain mechanisms’, Washington, DC: Spartan books.
Rumelhart D, Geoffrey H and Ronald JW (1985) ‘Learning internal representations by error propagation.’
Tibshirani R (1996) ‘Regression shrinkage and selection via the lasso’, Journal of the Royal Statistical Society Series B: Statistical Methodology 58.1: 267-288.
Zou H and Trevor H (2005) ‘Regularization and variable selection via the elastic net’, Journal of the Royal Statistical Society Series B: Statistical Methodology 67.2: 301-320.