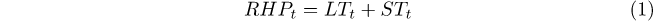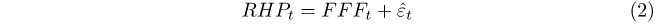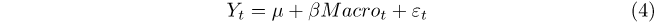We then examine the relation between both components and each of the macroeconomic variables.
3.1 Methodology
The FFF can be applied as a smoothing function to extract a long-run non-linear trend. Unlike conventional trend estimators, such as linear or quadratic, the FFF remains agnostic with respect to the trend’s form. This is advantageous, as, for example, a movement that appears to be a shock away from a linear trend may in fact be an underlying non-linear shift.
Li (2021) estimates the risk premium in financial markets by decomposing the observed risk premium into the actual risk premium, which is smooth and time-varying, and a short-term idiosyncratic error. We use a similar specification to define the long‑term and short-term components of real house prices as follows:
where RHPt is the value of the real house price index at time t, and LTt and STt are the long-term and short-term components of the index at time t respectively. We approximate the long-term component of real house prices using a fitted FFF, as follows:
where μ is an intercept term, n is the number of frequencies selected, T is the number of observations, and ak and bk are the coefficients estimated via OLS. The FFF approximates the long-term trend of the series, while the residuals εt from equation (2) approximate short-term fluctuations around the trend.1
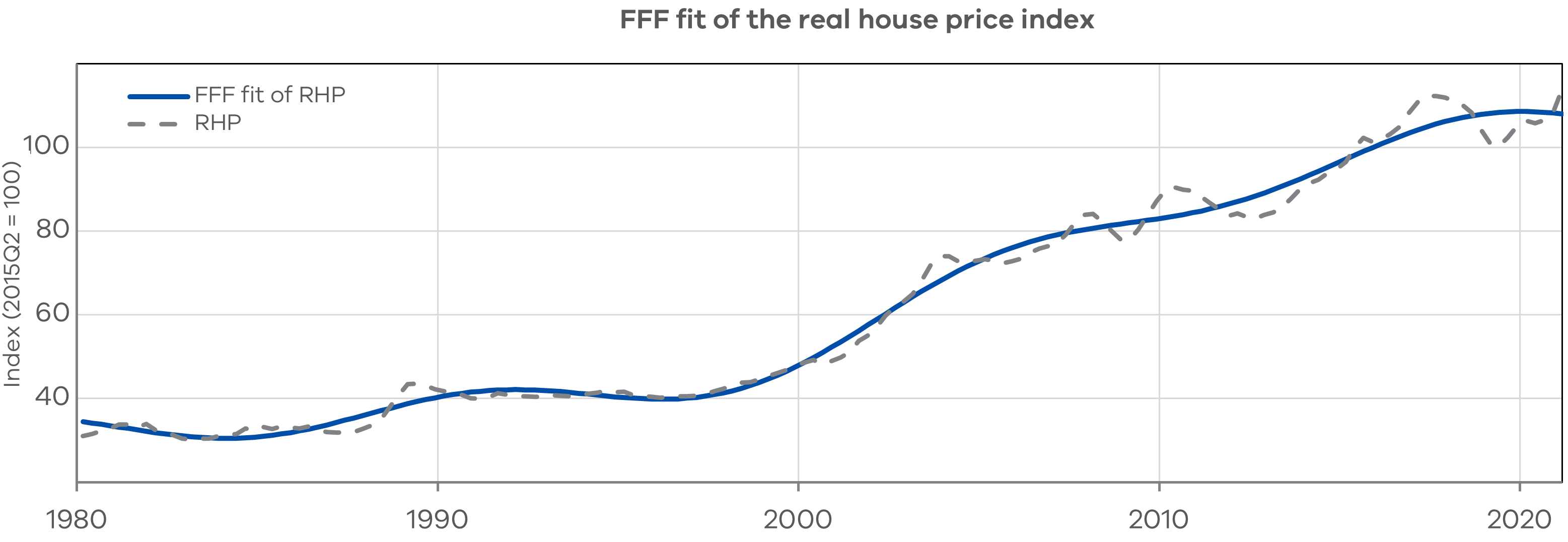
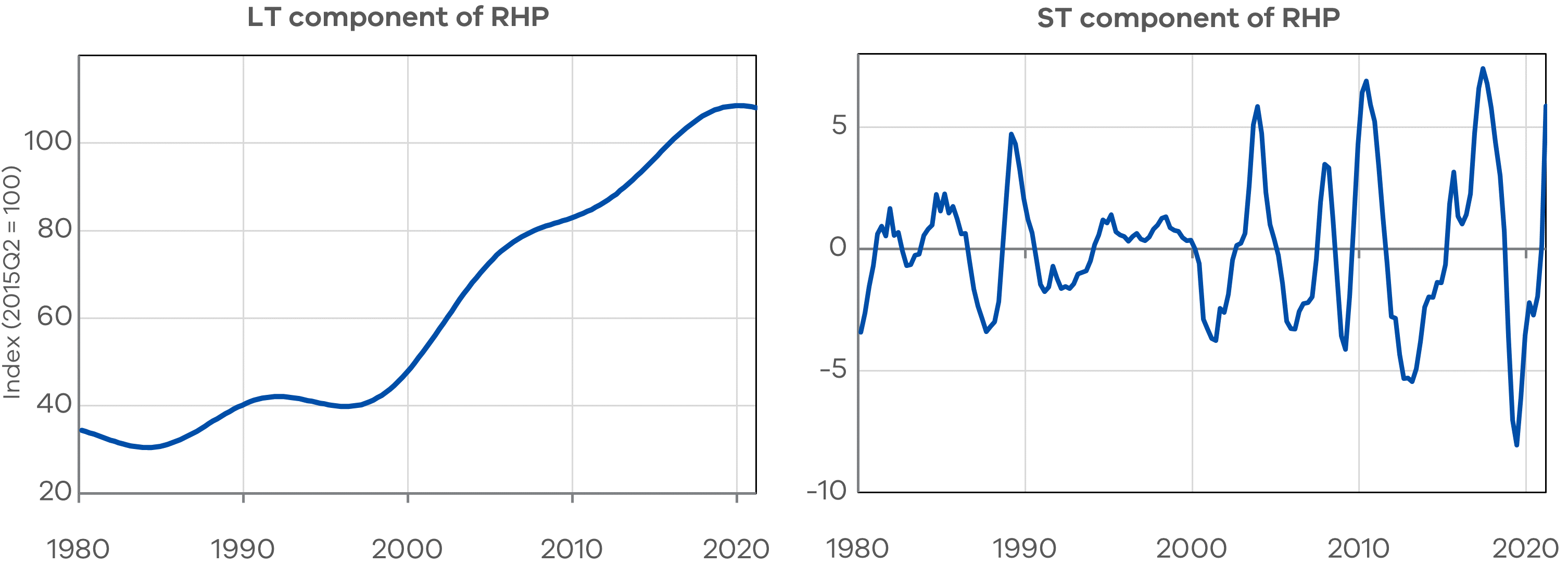
The results of the decomposition are shown in Figure 1. Visually, the FFF successfully approximates the non-linear trend, which displays significant growth over the period. In contrast, the short-term component displays cyclical behaviour, with periods above or below the trend generally persisting for two to five years.2
Figure 1: The decomposition of the LT and ST components of RHP in levels
Note: The smoothed function taken as the long-term component is generated by fitting the 3‑frequency Flexible Fourier Form to the RHP series. The ST component is the residual series from the regression, representing fluctuations around the long-term trend.
3.2 Long-term component
We perform Engle-Granger cointegration tests to determine if there are any long-run relationships between house prices and each of the macroeconomic variables. Tests are performed using the raw real house price index and the long-run component extracted via the FFF. We therefore examine whether removal of the short‑run component helps to better identify long‑run relationships between house prices and each of the macroeconomic variables. More specifically, cointegration is present if residuals from the following regression:
are I(0), where Yt is real house prices or its long-run component at time t, and Macrot denotes a macroeconomic variable at time t. Table 2 reports the results from these tests.
Table 2: Results for the pairwise Engle-Granger tests for cointegration
| Raw Levels | LT Levels | |||
| Rent price index | -1.85 | (0.61) | -4.34*** | (0.00) |
| Price-income ratio index | -2.39 | (0.33) | -3.64** | (0.02) |
| Price-rent ratio index | -2.94 | (0.12) | -2.20 | (0.42) |
| Cash rate | -1.22 | (0.85) | -1.28 | (0.84) |
| Exchange rate index | 0.54 | (0.99) | -0.90 | (0.92) |
| Sales volume | -1.19 | (0.86) | -0.93 | (0.92) |
| Real GDP | -3.43** | (0.04) | -2.82 | (0.16) |
| Real GDP PC | -2.40 | (0.33) | -2.38 | (0.34) |
| Disposable income | -3.45** | (0.04) | -4.00** | (0.01) |
| Disposable income PC | -2.54 | (0.26) | -2.60 | (0.24) |
| Population | -2.45 | (0.30) | -2.04 | (0.51) |
| Unemployment rate | -2.24 | (0.40) | -2.45 | (0.30) |
| Employment-population ratio | -2.38 | (0.33) | -2.50 | (0.28) |
| Participation rate | -2.13 | (0.46) | -2.24 | (0.40) |
| Consumer price index | -2.46 | (0.30) | -2.57 | (0.25) |
Note: the first and third columns show the T-statistics from the tests, and the numbers in parentheses are the corresponding p-values. Significance: 10%*, 5%**, 1%***.
Table 2 reveals that both the raw series and the long-term component of real house prices cointegrate with real disposable income. However, our results indicate that neither series cointegrate with real disposable income per capita. This suggests that although there may be a stable long-term relationship between house prices and disposable income, this does not hold when income is measured in per capita terms. A similar observation can be made for real GDP and real GDP per capita in the results for the raw series – prices share a stable relationship with overall real GDP, but not real GDP per capita.3 This suggests that real house price growth has outpaced income growth per person, and that a significant part of the growth in disposable income and GDP has occurred because of population growth. This has fuelled income growth overall, keeping the relation between income and real house prices stable.
An interesting finding is the detection of cointegration between real house prices and the rent price index once the FFF has been applied to remove fluctuations. This suggests that over the long-term, rents and prices tend to move together. Similarly, the FFF decomposition reveals a relationship between the long-term component of prices and the price-income ratio, an affordability measure capturing the ratio of nominal house prices to nominal disposable income per person. This is consistent with our finding of no cointegration with the per capita GDP or disposable income above. This points to houses having become less affordable as house price growth has outpaced per capita income growth.
Finally, it is worth mentioning that there is no long-run relation between house prices and sales volume. However, we will see that volumes have a strong relation with the short-term component of house prices.
In summary, the long-term component of RHP has a stable long-run relation with macroeconomic aggregates like disposable income and GDP, as well as rent and affordability, but these relations may be unidentified in the presence of short-term (possibly noisy) fluctuations in house prices. The long-run relation between RHP and income (i.e. disposable income or real GDP) does not hold when either income measure is on a per capita basis. This is due to a non-trivial part of the growth in income being due to population growth.
3.3 Short-term component
Figure 1 reveals that the short-term component displays cyclical behaviour around the nonlinear trend, with deviations above or below the trend lasting around two to five years. Because the short-term component is I(0), we use an Autoregressive Distributed Lag (ARDL) model. This enables us to explore any correlation or predictive relationships with other variables, using a mix of I(0) and I(1) variables.4 We set the number of lags on the dependent variable to one and use the SIC to determine the number of lags for each regressor, up to a maximum of four.
Table 3: The estimation results from seven ARDL regressions
| Dependent variable: Short term component of real house price index (levels) | |||||||
| Variable | (1) | (2) | (3) | (4) | (5) | (6) | (7) |
| SR component of RHP(-1) | 0.908*** | 0.893*** | 1.045*** | 1.030*** | 0.911*** | 1.023*** | 1.049*** |
| Cash rate | -0.026 | -0.011 | 0.019 | 0.047 | 0.151 | 0.024 | |
| Cash rate (-1) | -0.232** | ||||||
| Exchange rate | 0.112*** | 0.023*** | 0.032*** | ||||
| Exchange rate (-1) | 0.000 | ||||||
| Exchange rate (-2) | -0.110*** | ||||||
| Disposable income PC | 0.158 | -0.089 | |||||
| Disposable income PC (-1) | -0.132 | ||||||
| Disposable income PC (-2) | -0.449 | ||||||
| Disposable income PC (-3) | -2.216*** | ||||||
| Disposable income PC (-4) | 2.523*** | ||||||
| Sales volume | 0.051* | 0.063** | 0.065** | 0.049* | |||
| Sales volume (-1) | 0.145*** | 0.145*** | 0.145*** | 0.145*** | |||
| Sales volume (-2) | -0.004 | -0.003 | -0.005 | -0.005 | |||
| Sales volume (-3) | -0.059 | -0.059 | -0.060 | -0.059 | |||
| Sales volume (-4) | -0.112*** | -0.108*** | -0.098*** | -0.113*** | |||
| Constant | 0.234 | 0.046 | -0.897 | -3.120*** | 2.053** | -2.717** | -0.568* |
| R-squared | 0.802 | 0.825 | 0.887 | 0.892 | 0.834 | 0.899 | 0.886 |
| Adjusted R-squared | 0.800 | 0.820 | 0.882 | 0.886 | 0.825 | 0.892 | 0.882 |
| SIC | 3.387 | 3.357 | 2.999 | 2.986 | 3.415 | 3.003 | 2.970 |
| AIC | 3.330 | 3.243 | 2.846 | 2.814 | 3.242 | 2.811 | 2.836 |
The variables used are as follows. Cash rate: the interbank overnight cash rate in percent. Exchange rate: the trade weighted exchange rate index for the Australian dollar. Disposable income PC: the real net disposable income per capita in Australia, in 1000s of AUD. Sales volume: housing sales volume per quarter, in 1000s of units. Models are selected with SIC. All variables are integrated of order 0 or 1 according to the Augmented Dickey-Fuller test. Significance: 10%*, 5%**, 1%***.
Table 3 presents results from seven ARDL specifications. In all regressions, the autoregressive coefficient is significant at 1 per cent and highly persistent. This is consistent with sustained periods above or below the long-run trend. The most notable result from these regressions is the highly significant coefficients on both the contemporaneous and lagged values of sales volume in regressions (3), (4), (6), and (7). These coefficients remain significant even when the cash rate, the exchange rate, and disposable income are included as additional regressors, indicating that sales volume may be highly predictive of short-term fluctuations in real house prices. There may be some cyclical behaviour being captured by the positive coefficients for the contemporaneous and first lag values, and by negative coefficients for longer lags.
The cash rate is not significant contemporaneously in any of the regressions. However, its first lag is negatively correlated with the short-term component at the 5 per cent level in regression (5). The predictive relationship of the cash rate on short‑term fluctuations may come through its influence on exchange rates, which is significant at the 1 per cent level in regressions (2), (4), and (6). Disposable income per capita does not have a contemporaneous relationship with the short-term component, but regression (5) shows that it may be predictive at three or four lags. However, this relationship disappears when sales volume and the exchange rate are accounted for in regression (6).
Of the six regressions, regression (7) minimises the SIC, and has the third-lowest AIC, suggesting that it is the best explanatory model for the short-term component of real house prices. This model only includes sales volume, indicating that it may be one of the most important predictors of short-term fluctuations in the Australian housing market. Regression (4) also features a low SIC and AIC, suggesting that perhaps the cash rate and trade-weighted exchange rates are helpful at predicting short-term fluctuations.
In summary, the decomposition of house prices into long-term and short-term components enables us to uncover additional macroeconomic linkages with house prices. Cointegration or long-term relationships are seen between real house prices and income (disposable income and real GDP), rents, and the price-to-income ratio. When income is on a per capita basis, there is no longer a stable long-run relation with house prices. The ARDL models suggest that sales volume has a strong contemporaneous and lagged relationship with house prices in the short-term, which is consistent with Zhou (1997).
Footnotes
[1] We limit the number of trigonometric frequencies (n) in equation (3) to a maximum of three. This means that a smoother fit is generated, thereby better approximating the overall trend without capturing short‑term fluctuations. Three frequencies are ultimately selected, as this minimises the Schwarz Information Criterion (SIC) for the regression on equation (3), compared to one or two frequencies.
[2] We also extract the long-term and short-term components of real house prices in logs as this helps remove some of the nonlinearities by reducing the impact of large fluctuations. The results are similar.
[3] Prices are no longer cointegrated with real GDP once the FFF has been applied, but due to the lack of power of the ADF test, there may still be a relationship with real GDP (p-value of 0.16), but there is unlikely to be one with real GDP per capita (p-value of 0.34).
[4] We are careful not to make any causal interpretation, as this requires weakly exogenous independent variables. Significant coefficients can also be the result of spurious regression if the ARDL bounds test indicates no cointegration. Interpretation must be mindful of omitted variables and other sources of endogeneity that may bias the results.
Updated