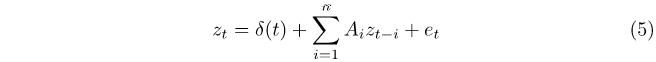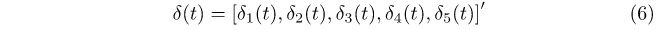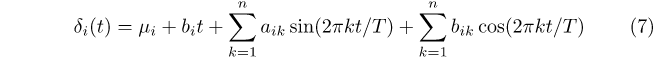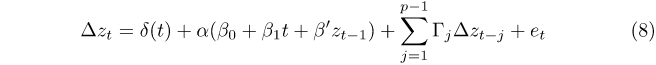The literature generally points to the importance of both forms of structural break when modelling house prices. Droes et al. (2016) find a shift over time in the importance of different variables (population growth, new housing supply, income, interest rates) on the housing market in Amsterdam. Aye et al. (2013) identify structural breaks in the South African housing market and control for these via Structural Vector Autoregression (SVAR). A strengthening of the relationship between US house prices and macroeconomic variables (private consumption and economic activity) is found by Ahamada and Diaz Sanchez (2013). Muellbauer and Murphy (1997) model structural breaks in the bivariate relation between house prices and income and house prices and interest rates.
The most common ways to account for structural breaks are breakpoint regression, threshold regression and Markov switching. All of these approaches tend to be heavily parameterised, as each additional regime requires estimation of a new set of parameters. To maintain tractability, very often the number of regimes is small. Markov switching models, for example, very often limit the number of regimes to two, otherwise estimation issues, such as failure to converge or sensitivity of estimates to starting values, often arise. Breakpoint and threshold regression also require breakpoint identification, and threshold regression requires a suitable threshold variable. An alternative to these models is to use a dummy variable approach. Enders and Jones (2016) identify that these approaches can be effective when there are a small number of sharp breaks or additive outliers but will not be as capable of detecting mean shifts if the breaks are sufficiently smooth (innovative outliers).
The FFF overcomes all of these limitations. Allowing for structural change via the FFF does not require breakpoint, regime, or dummy identification, and when incorporated into a VAR, the model can still be easily estimated via OLS. To our knowledge, we are the first paper to control for structural breaks in the Australian housing market in this way.
The use of the FFF to control for structural breaks is a recent development, so academic studies are limited. Enders and Jones (2016) incorporate the FFF into a VAR between oil and grain prices. They note that structural breaks within a VAR are generally more complicated to deal with than in a univariate setting due to the interrelationships between variables. It can be difficult to determine if a break in one of the variables is due to a break in its own series, or whether it is a break that is being transmitted from one of the other series.
The results of Enders and Jones (2016) confirm Ng and Vogelsang’s (2002) finding that Granger-causality tests are mis-sized when structural breaks are unaccounted for. As a result, they find that Granger-causality tests identify much richer relationships between variables when employing the FFF. They also show additive and innovative outliers can be controlled for by the FFF, and that it can effectively capture sharp and smooth breaks. This contrasts with Bai and Perron’s (1998) methodology, which performs poorly in the presence of smooth breaks. Given the housing market frictions discussed earlier, structural breaks are likely to be smooth, so the FFF seems a prudent way to proceed.
4.1 Methodology
In this section, we examine the impact of controlling for structural breaks via the FFF when modelling Australian house prices. For robustness and comparative purposes, we consider a VAR in levels with a time trend, a VECM, and a VAR in first-differences.1 We compare the standard version of each model, which does not control for breaks, with the FFF version of the model, which does control for breaks. To examine model differences, we focus on Granger-causality tests, as they are mis-sized in the presence of breaks.2 All models select the optimal lag via the Schwarz Information Criterion. Our choice of variables is based on our analysis in Section 3 and contemporary literature.
The FFF-VAR is specified as:
where zt is a (5 × 1) vector (RHP, cash rate (%), disposable income per capita ($000’s), sales volume (000’s), unemployment rate (%)), Ai is a (5 × 5) coefficient matrix for lag i, et is a (5 × 1) vector of error terms and all variables are in levels. The δ(t) term in equation (5) is defined as:
with each time-varying intercept δi(t) depending on n Fourier frequencies in the following way:
where μi is a constant, bit is a linear time trend, T is the total number of observations in the sample, and aik and bik are coefficients on the trigonometric terms. We use the SIC to jointly select the lag length and the order of the FFF for our models. For this VAR, a lag length of 1 and a trigonometric order of n = 3 is selected. Conventional VARs without the FFF are nested within the FFF-VAR. A non-FFF VAR with a linear time trend imposes aik=bik=0 for all i and k, and a VAR in first-differences additionally imposes bit = 0.
The FFF-VECM is specified as:
with the same definitions as the FFF-VAR above. Γj is a (5 × 5) coefficient matrix for lag j. The time varying intercepts within δ(t) do not include a time trend, that is, bit = is imposed. As above, the conventional VECM is specified in the same way, but with the additional restrictions of aik = bik = 0. This specification (restricted intercept and restricted trend in the cointegrating vector) is selected as it should be used in the presence of deterministic and stochastic trends (Johansen 1995). RHP, the cash rate and the unemployment rate are likely to have stochastic trends, but sales volume is much more likely to grow deterministically over the long run with population.
4.2 Results
Table 4 presents Granger-causality tests for the six models. Parameter estimates and other details for all models are available on request. Panels A, C, and E show the models without the FFF, whereas panels B, D, and F show the FFF-augmented versions of each model. Sales volume clearly Granger-causes (GCs) house prices in all VARs. Real house prices also GC sales volume in all models, but not to the same degree. The cash rate and unemployment rate both GC each other in every model. The unemployment rate GCs real house prices at the 1 per cent level in two of the FFF models (panels B and F), but that relationship is not detected in the other models.
Comparing panels A and B, it is clear that the FFF-VAR can detect Granger- causal relationships that the linear VAR is unable to capture. For instance, only sales volume Granger-causes RHP in panel A, but both disposable income per capita and the unemployment rate Granger-cause RHP at the 5 per cent level or better in panel B. A similar result is seen in panels E and F, with the FFF-VECM detecting relationships that the regular VECM fails to find. Panels C and D are very similar in their detection of Granger-causal relationships, indicating that the FFF is not as important when the data is differenced. These results are consistent with the findings of Enders and Jones (2016), who show that unaccounted structural breaks can cause Granger-causality tests to be mis-sized. Panels B and F detect more economically sound relationships than panels A and E respectively, as they control for structural breaks using the FFF. The same effects are clearly not present in the first-difference models. This is consistent with structural breaks in long‑term dynamics that are removed by differencing.
We now compare the impulse response functions for real house prices in Figure 2. In the interest of brevity, we only present three models: the FFF-VECM, the FFF-VAR with linear trend, and the regular VAR in first-differences.3
Table 4: Granger-causality results from the six models examined
| RHP | CR | DI PC | SV | UR | |
| A: VAR in levels with time trend | |||||
| Real house prices | – | 6.54** | 2.27 | 16.18*** | 3.94 |
| Cash rate | 1.35 | – | 3.18 | 1.91 | 12.41*** |
| Disp. inc. PC | 0.28 | 1.17 | – | 5.14* | 2.09 |
| Sales volume | 59.75*** | 2.64 | 2.32 | – | 3.64 |
| Unemployment rate | 2.00 | 11.53*** | 3.34 | 7.01** | – |
| B: FFF-VAR in levels with time trend | |||||
| Real house prices | – | 10.76*** | 2.19 | 19.49*** | 8.44*** |
| Cash rate | 0.54 | – | 4.12** | 0.08 | 9.80*** |
| Disp. inc. PC | 6.41** | 0.97 | – | 0.04 | 0.66 |
| Sales volume | 163.02*** | 0.54 | 0.25 | – | 4.73** |
| Unemployment rate | 12.87*** | 33.52*** | 5.41** | 1.71 | – |
| C: VAR in first-differences | |||||
| Real house prices | – | 4.59** | 0.04 | 6.36** | 5.77** |
| Cash rate | 0.51 | – | 0.55 | 1.64 | 5.23** |
| Disp. inc. PC | 0.32 | 0.67 | – | 3.05* | 2.07 |
| Sales volume | 66.33*** | 0.58 | 1.44 | – | 4.35** |
| Unemployment rate | 1.16 | 8.24*** | 1.39 | 5.09** | – |
| D: FFF-VAR in first-differences | |||||
| Real house prices | – | 4.72** | 0.00 | 5.47** | 5.28** |
| Cash rate | 0.55 | – | 0.63 | 1.65 | 5.62** |
| Disp. inc. PC | 0.21 | 0.59 | – | 3.14* | 1.92 |
| Sales volume | 68.73*** | 0.61 | 1.55 | – | 4.29** |
| Unemployment rate | 1.08 | 8.55*** | 1.23 | 5.00** | – |
| E: VECM in levels | |||||
| Real house prices | – | 9.30*** | 0.06 | 0.34 | 6.50** |
| Cash rate | 0.59 | – | 0.57 | 0.42 | 5.81** |
| Disp. inc. PC | 0.35 | 0.37 | – | 4.66** | 2.30 |
| Sales volume | 65.92*** | 0.28 | 1.46 | – | 4.69** |
| Unemployment rate | 1.25 | 6.35** | 1.29 | 8.34*** | – |
| F: FFF-VECM in levels | |||||
| Real house prices | – | 2.25 | 7.15** | 15.96*** | 2.72 |
| Cash rate | 4.99* | – | 5.60* | 0.02 | 6.79** |
| Disp. inc. PC | 6.05** | 0.01 | – | 4.84* | 9.30*** |
| Sales volume | 37.04*** | 5.20* | 2.88 | – | 4.40 |
| Unemployment rate | 9.37*** | 7.23** | 7.04** | 5.57* | – |
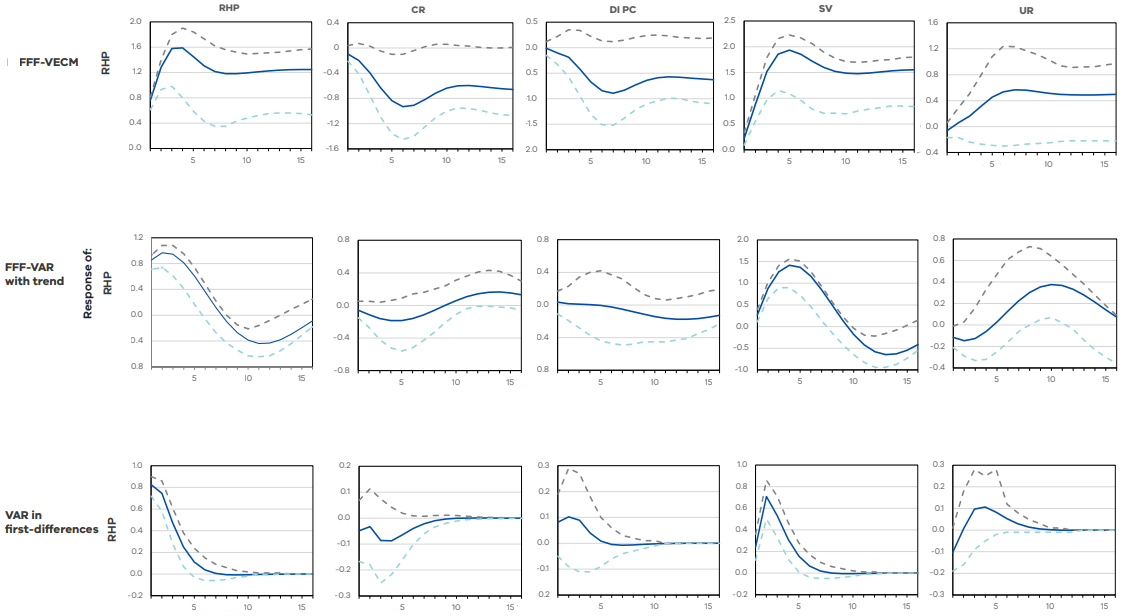
Figure 2: The generalised impulse responses of real house prices
Response to generalised one S.D. innovations
95% CI using standard percentile bootstrap with 1000 bootstrap reps
Shock to:
Note: shown are the generalised impulse responses of real house prices to a one standard deviation shock for each of the variables in the system. The FFF-VECM is in row 1, the FFF-VAR with linear trend is in row 2, and the VAR in first-differences is in row 3. The solid line shows the impulse response, and the dashed lines show the 95 per cent confidence interval using the standard percentile bootstrap with 1000 replications. Variables are as follows. RHP: Real house price index, CR: Interbank overnight cash rate, in per cent, DI PC: disposable income per capita in thousands of AUD, SV: housing sales volume in thousands of units, UR: unemployment rate in per cent. The shock is at period 0, and 16 periods are shown in each graph.
There is a notable difference in the size and persistence of the impulse responses from the FFF-VAR and FFF-VECM compared to the linear VAR in first‑differences. This is to be expected, as differencing removes the long-run dynamics.4 We also note that the higher levels of persistence to shocks in the VECM is due to the cointegrating relation between variables that is not present in the VAR in levels.
The FFF-VECM suggests that a positive shock to real house prices will be persistent over the following four years, but the FFF-VAR IRF implies that a correction may occur after approximately 10 quarters. Both the FFF-VAR and FFF-VECM IRFs show that a positive shock to the cash rate does not have a statistically significant effect on real house prices, although the FFF-VECM suggests a small downward movement could occur. Disposable income per capita does not have a statistically significant effect on prices in all three models. Sales volume has a large impact on house prices, with all three models indicating that prices will increase for at least a year after a positive volume shock. This is consistent with the ARDL findings in Section 3.3. The FFF‑VECM suggests this effect will be persistent for at least four years, while the FFF‑VAR suggests a slight correction after two years. Finally, a shock to the unemployment rate does not have a significant effect on prices in any of the models, although there is some indication in the FFF-VAR model that this shock could cause a delayed increase in prices after two years. This is likely due to the easing of monetary policy in response to a weakening economy and labour market.
Footnotes
[1] We also test a VAR in levels without a time trend, but this model has been discarded due to roots within the unit circle.
[2] We also examine the Granger-causality results for the VECM in logs and VAR in log first-differences, reported in the appendix. The linear VAR in logs has inverse roots outside of the unit circle even with the inclusion of a time trend, so it is not reported.
[3] The regular VAR and VECM show similar IRFs to their FFF counterparts, but the size and significance of the impulses is reduced, consistent with these models’ inability to fully capture variable interrelationships when structural breaks are present.
[4] While first-differencing can mitigate some of the issues caused by the presence of structural breaks, namely mis-sized Granger-causality tests, we are certainly not advocating the abandonment of the VAR or VECM in levels given the importance of long-run dynamics in the economy.
Updated