- Published by:
- Department of Treasury and Finance
- Date:
- 1 Aug 2022
Rebecca Valenzuela1,2
1 Revenue Forecasting Team, Economic Division, DTF.
2 Author contact details: veb@dtf.vic.gov.au
Acknowledgements: The author would like to thank Omid Mousavi, Michael Woods, Andrew O’Keefe, Helen Ratcliffe, Jeff Borland and attendees at the interagency seminar series for their comments. Also thanks to Edward Jin for his excellent help with the HILDA data extraction.
Disclaimer: The views expressed in this paper are those of the authors and do not necessarily reflect the views of DTF.
Suggested Citation: Rebecca Valenzuela (2022) Duration modelling of education effects and gendered outcomes in the Australian graduate labour market. Victoria’s Economic Bulletin, August, vol 6, no 2. DTF.
Abstract
This study examines and compares the labour market outcomes of tertiary-educated men and women in Australia using duration modelling techniques. It confirms the existence of gaps between men and women in the Australian graduate labour market and identifies a number of likely causes of their persistence over time. Our main findings suggest that after graduation, women take more time than men to find full-time employment and to achieve important benchmarks in the workplace. We find that traditional gender roles in the home continue to prevent women from progressing at the same pace as men and maximising the career benefits of higher education. Expanding education is clearly a step in the right direction for the Government, but the data shows that this alone is not enough to address the persistence of gender gaps. A realignment of gender roles and perceptions in all corners of society – in the home, in schools and in workplaces – is needed to consolidate gains on the education front. In terms of policy, our results imply that education initiatives should be complemented by structural reforms in the labour market to properly address the gender gap and assist families in managing imbalances in particular times of the life cycle.
1. Introduction
Education has been long recognised as an important tool for improving labour market outcomes.
Education has been long recognised as an important tool for improving labour market outcomes, such as earnings and employment, as well as non-market outcomes such as health, longevity, civic participation and criminal activity.1 More recently, governments have used education to improve gender equality, not only out of concerns for fairness, but also because it is linked to a country's overall economic performance. More gender-equal workplaces, industries and occupations have been shown to have higher levels of workforce productivity. Reductions in gender inequality are also linked to strong or accelerated economic growth.2 Despite this, gender-based gaps in economic and social outcomes persist in many societies.
In the labour market, it remains unclear how policy efforts to reduce gender gaps in education impact on employment outcomes, which, by and large, continue to be unfavourable for women.3 This is mainly because of conflicting results borne out by studies that use different data sets or measures and models and employ divergent methodological approaches to econometric modelling issues. This means that even when there is a sound theoretical framework for how gender gaps in education impact on economic growth, the empirical evidence for testing how this relationship manifests in the labour market has not been straightforward.4
The case of Australia presents an interesting conundrum. In 2020 and in 2021, the World Economic Forum (WEF) ranked the country first in gender equality in educational attainment, which means Australia has closed the education gender gap ahead of the 150 countries that were covered in the report (WEF 2020; WEF 2021). However, the 2021 WEF report ranked Australia 70 out of 150 countries in terms of equality in economic performance and opportunity, down 21 places from 2020.5 The clear implication is that Australia’s success in achieving gender equality in education is not translating into better outcomes for women in the labour market. This raises concerns on both moral and economic fronts. Society has a moral imperative to ensure that women have, in equal measure as men, access to the right to work by choice and in conditions of dignity, safety and fairness. At the same time, reducing gender gaps in the labour market could also substantially boost gross domestic product, accelerate sustainable growth and development, and improve living standards for all (Nica 2019; Nguyen 2021; Lagerlöf 2003).
This paper uses duration modelling techniques to gain insight into the country’s graduate labour market and analyse why gender inequality persists despite strong education outcomes. Data from the Household, Income and Labour Dynamics in Australia survey (HILDA) is used to understand the role of higher education in employment outcomes and examine education underutilisation in the Australian graduate labour force. Overall, this study aims to identify the market and non-market factors that drive the disparity between tertiary-educated men and women in labour market outcomes.
Duration modelling has been used many times before to analyse labour market transition issues, but none of these studies have used this approach to explain differential labour market outcomes for tertiary-educated men and women. While duration modelling studies of labour market outcomes rarely distinguish between outcomes for men and women, some can provide useful starting points for our paper. For instance, Nickell (1979) finds that in the UK, each year of schooling up to 12 years reduces the expected duration of unemployment by over 4 per cent, and that the acquisition of qualifications beyond ordinary level (i.e. secondary) reduces the expected unemployment duration by 12 per cent. Farber (2004) finds that among people who have recently lost jobs, those with higher levels of education have higher post-displacement employment rates and are more likely to be re-employed full-time.
To our knowledge, this study is the first to systematically investigate labour market inequalities between tertiary-educated men and women in Australia using duration modelling techniques. By tracking individuals over a period of years, the paper describes how tertiary-education may increase opportunities for individuals, using such measures as shorter spells of unemployment after graduation, increased probability of landing full-time jobs and better matching of job requirements to training background. It also contributes to the literature on the private and social benefits of investing in tertiary-level education. Results from this study provide a deeper understanding of the role of higher education in achieving gender equity in the Australian labour market, which can help in designing policy strategies to address gendered labour market issues in the long term.
Section 2 presents the conceptual framework and reviews the relevant economic literature. Section 3 discusses the duration modelling approaches used. Section 4 presents the data and summary statistics. Section 5 presents results from the Kaplan-Meier method. Section 6 presents the results and discusses the impact of covariates from the Cox Proportional Hazard regression model approach. Section 7 concludes.
Footnotes
[1] Card (2001); Grossman (2005); Oreopoulos and Salvanes (2009); Machin et al. (2011).
[2] See Klasen (2018) for a recent cross-country comparison. Also, Benos and Zotou (2014) for an exhaustive survey of the literature on the
impact of gender inequality on growth.
[3] In their meta-regression analysis of 57 studies, Benos and Zotou (2014) could not claim consensus.
[4] See Lucas (1988), Lagerlof (2003) and Stotky (2006) for excellent discussions on alternative theoretical models.
[5] Australia ranked 44th and 50th overall in 2020 and 2021; For 2020 and 2021, Australia ranked 104th and 99th in Health and Survival dimension, respectively, and 57th and 54th in the political empowerment dimension, respectively. Overall, considering all the four components, the ranking of Australia in the Global Gender Gap Index was 44 in 2020 and 50 in 2021 (WEF 2020; WEF 2021).
2. Review of literature
Gender inequity in the Australian labour market has been extensively studied in the past.
Most of the early work in the field attempted to explain gender wage or earnings gaps in the local labour market. The long run trends show that the gender wage gap narrowed considerably in the 1970s following the 1969 and 1972 equal pay cases and stabilised to between 15 and 20 per cent since the early 1980s (Borland 1999). In terms of causes, early studies such as Miller (1994) and Wooden (1999) identified occupational segregation as the key factor in observed gender-wage differentials – specifically, they showed that wages were lower in women-dominated occupations. Subsequent studies such as those of Lee and Miller (2004), Baron and Cobb-Clark (2010) and Cobb-Clark and Tan (2011), however, found that occupational segregation is in fact not a significant determinant of gender wage gaps. A survey article by Coelli (2014) reconciled these results by showing that the impact of occupational segregation on gender wage differentials depended on the way occupations are grouped in the studies – specifically, the paper demonstrated that larger gender wage gaps are observed when occupations are classified at more detailed levels. More recently, Borland and Coelli (2016) showed that occupational segregation in Australia has fallen over time, a result which aligned Australian experience with those of other advanced economies. Their analysis of longer-term data also revealed that occupations where men and women are concentrated have changed substantially over time, and that women tend to move from low-skill to high-skill occupations, while men primarily move from middle-skill to high-skill occupations, but also somewhat to low-skill occupations.
The glass ceiling effect has also attracted heavy attention from labour economists as a plausible explanation for observed gender wage differentials. Glass ceiling is a term used to refer to a set of office-wide policies, practices, attitudes and traditions in a society that prevent women from rising to the top positions in a firm. Miller (2005) and Kee (2006) were among the first to empirically demonstrate that the equality of earnings/wages of men and women in Australia are constrained by a glass ceiling and that this effect is more pronounced in the graduate labour market where wages are relatively high. Using a larger pool of more recent data from the Household, Income and Labour Dynamics in Australia (HILDA) Survey, Baron and Cobb-Clark (2010) confirmed the existence of a glass ceiling in the Australian labour market and added that it is more pronounced in the private sector than the public sector.
On studies that examine the impact of unemployment duration on gender inequality, findings from some recent research may be worth mentioning even if these studies are not necessarily focused on the tertiary-qualified workforce. Theodossiou and Zangelidis (2009) found that men switch from job-to-job more easily than women and that labour market transitions for women are less from job-to-job and more from job-to-unemployment. They also find that higher levels of education reduce the likelihood of transitioning from job to unemployment, particularly for women. Gokulsing and Tandrayen-Ragoobur (2014) found evidence that employers do prefer men over women even if women have higher education or if men have lower education and performance. Mitri (2021) meanwhile demonstrates that regardless of their educational attainment, women are more likely to be precariously employed compared to men and that higher education does not improve wage earnings for men or women within precarious work. All in all, these studies agree that higher levels of education resulted in a wage penalty for men, whereas women earned a wage premium at lower levels of educational attainment.
3. Duration modelling
This study employs survival analysis techniques to compare durations of unemployment and other economic outcomes between tertiary-qualified men and women in Australia.
This technique is ideal for our purposes because we are studying an economic outcome that takes time to eventuate. Specifically, it enables analysis of the varying lengths of time for individuals to achieve particular labour market outcomes, such as finding a full-time and/or secure job, after the completion of tertiary studies. It is advantageous because it allows gender-based unemployment patterns to be studied temporally. In this framework, ‘survival’ refers to being unemployed and ‘failure’ refers to finding a job or some other desired labour market outcome. The time a person spends in a given state (unemployment) is referred to as a ‘spell’ and the duration of a spell is considered a random variable. For a robust analysis, we employ two complementing approaches under duration modelling: (i) a non-parametric method called the Kaplan-Meier survival method and (ii) the Cox Proportion Hazard model, which is regression based.
3.1 Kaplan-Meier survival analysis
The Kaplan-Meier (KM) duration modelling technique is a non-parametric modelling approach that enables analysis through the estimation of a survival function (Kaplan and Meier 1958). To start, we define a ‘spell’ as a length of time that a homogenous group of persons experiences a state of being such as being alive or being in remission, being single or being married, being in foster care, being in detention, being unemployed or being a welfare recipient. We define an ‘event’ as the point in time when the person exits the spell. Using data, KM provides a survival rate, which is the person’s probability of staying in the spell or surviving the spell. KM also provides a hazard rate which pertains to a person’s probability of reaching the ‘event’ and exiting the spell.
In more technical language, the KM approach involves the estimation of a survival function defined as:
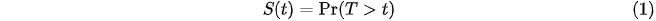
which gives the probability that a spell will last until a certain time t. T is a random variable that represents spell duration, while t represents the observed/actual duration. The function in (1) is formally interpreted as the probability of survival after time t. The cumulative distribution of T is denoted by:
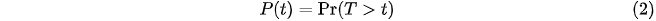
while:
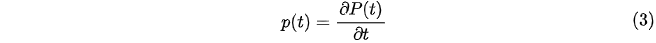
is the probability density function. Consequently, the survival function is:
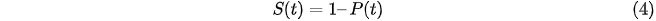
and the instantaneous probability of exiting a spell is calculated using the hazard function h(t) which is written as:
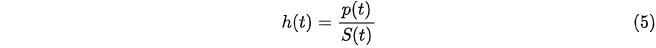
Since this study is about labour market outcomes, we default to full-time unemployment as the spell and our KM surviving function S(t) measures the probability of an individual remaining in full-time unemployment. An event is then defined as finding a full-time job, and the KM hazard rate indicates the person’s probability of exiting unemployment and finding a full-time job.1 The method allows for the estimation of a life table, and a graph, called survival curve, which are all produced for a better view of the population at risk.
3.2 Time varying covariates and Cox Proportional Hazard modelling
Survival regression analysis allows us to use the duration and the exit variables in the modelling exercises and also use additional data, such as age, gender, and wages, to serve as explanatory variables or what many also call covariates. There are several ways to implement this on data, but the most popular approach is the Cox Proportional Hazard (CPH) regression model. CPH modelling employs a distribution-free approach and calculates survival rates that only depend on the ranks of the event times, rather than on their numerical values. This means that any monotonic transformation of the event times will leave the coefficient estimates unchanged.
CPH regression modelling is similar to implementing a multiple regression analysis, with the key difference that the dependent variable is the hazard function h(t) at a given time t, rather than the conventional observed y variable. The model works such that the log-hazard of an individual subject is a linear function of their static covariates and a population-level baseline hazard function that changes over time. These covariates are estimated by partial likelihood, and as such, the approach is effectively a semi-parametric modelling exercise. The approach is semi-parametric in the sense that the baseline hazard function does not have to be specified. This allows the estimation to be fully flexible, in that a different parameter can be used for each unique survival time, while simultaneously assuming the rate ratio remains proportional throughout the follow-up period. The term ‘proportional hazards’ refers to the assumption of a constant relationship between the dependent variable and the regression coefficients. This implies that the hazard functions for any two subjects at any point in time are proportional – in other words, it assumes multiplicative effects of the covariates on the hazard function.
In this paper, the form of the Cox Proportional Hazards regression model is given as follows:
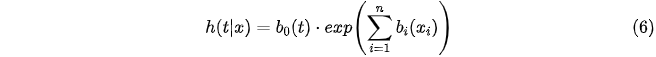
where b0(t) is the baseline hazard rate and indicates the probability of experiencing unemployment when all other covariates equal zero. The regression coefficients, bi(xi), give the proportional change that can be expected in the hazard h(t|x). A hazard ratio of 1.0 means that the covariate regressor has no effect on the hazard rate, a value less than 1.0 means that the covariate regressor reduces the hazard rate, and a value greater than 1.0 implies that the covariate regressor increases the hazard rate. Note that b0(t) is the only time-dependent component in the model. The sign of the regression coefficients, bi, also play an important role – a positive sign means that the risk of the event is higher, while a negative sign means that the risk of the event is lower. The model is estimated using maximum partial likelihood techniques.
Footnotes
[1] The terms survival and hazard appear counter-intuitive at first, and at first pass, they actually are. This comes from the fact that duration modelling has its roots in the medical field where duration spells often refer to the length of time a patient lives and survives, and the exit event is death, hence the term hazard rate for what most would consider a negative outcome. For this study, it will be helpful to bear in mind that ‘surviving’ means staying unemployed, which is a negative outcome, and that the hazard event is finding a job, which is a desirable and positive outcome.
4. Data: Sample overview and summary statistics
This study draws on the Household, Income and Labour Dynamics in Australia (HILDA) Survey.
This study draws on the Household, Income and Labour Dynamics in Australia (HILDA) Survey to examine the role of higher education on employment outcomes in the graduate employment market. The HILDA Survey tracks approximately 17 000 individuals in some 9 500 Australian households annually through time, beginning from 2001 when the survey was first conducted. We use HILDA survey waves from 2001 thru to 2018 to draw the sample of households used for this study.
This paper restricts analysis to those individuals who have obtained or completed a tertiary degree during the HILDA survey years. This group would include all those who completed a bachelor’s degree, an honour’s degree, a graduate diploma or certificate, a master’s degree or a PhD. Available data at the individual level include age, gender, marital status, health, ethnicity, education and employment. Available information on individuals’ jobs have also been used, including details on occupation type, industry type, broad conditions of contract as well as periods of unemployment or voluntary absence from the labour market and why. The total number of persons in the pooled sample is 14 192, which is equivalent to approximately 2030 unique individuals who appeared in the survey for a given period. The number of years that individuals are observed in the sample ranges from one year to 17 years, with a median of 6.5. This set of individuals will comprise the paper’s analytical sample, hereon simply referred to as the sample.
The distribution of the sample between genders across variables of interest are tabulated in Table 1. Across all people, the sample consists of 40 per cent men and 60 per cent women with ages ranging from 17 to 59 years.1 Seventy per cent of all people are aged 25 to 44 and close to 80 per cent live in major cities. All have completed at least a bachelor’s degree and close to a half have completed a postgraduate qualification as well. Further, 89.6 per cent of people in the sample are employed, 2.5 per cent are unemployed and the remaining 7.9 are classified as Not In Labour Force (NILF).2 This latter group consists of those who are not actively looking for work in the specified period, for various reasons, and includes a subset of people who are referred to as ‘discouraged job seekers’.
Table 1. Description of variables
| Variable | Male | Female | All | |
| Gender | 40.7 | 59.4 | N=14192 | |
| Age group | < 25 | 14.8 | 16.9 | 16.0 |
| 25-44 | 71.7 | 67.5 | 69.2 | |
| 45-64 | 13.5 | 15.7 | 14.8 | |
| Location | Urban | 18.9 | 23.1 | 21.4 |
| Rural | 81.1 | 76.9 | 78.6 | |
| Education (% row) | ||||
| - PhD/Masters | 41.7 | 58.3 | 100.0 | |
| - Grad Dip/Cert | 39.9 | 60.1 | 100.0 | |
| - Bachelors/Honours | 40.5 | 59.5 | 100.0 | |
| Education (% column) | ||||
| - PhD/Masters | 26.1 | 25.0 | 25.4 | |
| - Grad Dip/Cert | 22.2 | 22.9 | 22.6 | |
| - Bachelors/Honours | 51.7 | 52.1 | 51.9 | |
| LF Status (% row) | ||||
| - Employed | 42.4 | 57.6 | 100.0 | |
| - Unemployed | 43.2 | 56.8 | 100.0 | |
| - NILF | 19.7 | 80.3 | 100.0 | |
| LF Status (% column) | ||||
| - Employed | 93.5 | 86.9 | 89.6 | |
| - Unemployed | 2.7 | 2.4 | 2.5 | |
| - NILF | 3.8 | 10.7 | 7.9 | |
| LF status (employed only, % row) | ||||
| - Full-time | 46.0 | 54.0 | 100.0 | |
| - Part-time | 29.19 | 70.81 | 100 | |
| LF Status (employed only, % column) | ||||
| - Full-time | 77.1 | 62.1 | 68.2 | |
| - Part-time | 22.75 | 37.82 | 31.7 | |
| Job contract (among those employed; % row) | ||||
| - Fixed term | 34.32 | 65.68 | 100 | |
| - Casual | 36.38 | 63.62 | 100 | |
| - Permanent | 44.6 | 55.4 | 100 | |
| - Other | 30.77 | 69.23 | 100 | |
| Job contract (among those employed; % column) | ||||
| - Fixed term | 14.38 | 19.77 | 17.51 | |
| - Casual | 10.2 | 12.82 | 11.72 | |
| - Permanent | 75.25 | 67.15 | 70.54 | |
| - Other | 0.16 | 0.26 | 0.22 | |
| Industry | ||||
| - Construction | 80.74 | 19.26 | 100 | |
| - Mining | 67.55 | 32.45 | 100 | |
| - Transport, postal and warehousing | 72.78 | 27.22 | 100 | |
| - Education and training | 29.17 | 70.83 | 100 | |
| - Health care and social assistance | 22.3 | 77.7 | 100 |
Details in the labour force status of the sample present further distinctions along gender lines. Among all who are employed, seven in every 10 work full time, while the rest work in a part-time capacity. Seventy-seven per cent of men surveyed are in full-time jobs compared to 62 per cent of the women. Eight in every 10 people working part-time are women, who mostly cite childcare as the main reason for working part-time. In contrast, among part-time workers who are men, only 5 per cent cited childcare as the main reason for being in part-time work, while over 40 per cent of men in part-time positions cited other non-care personal or family obligations as their main reason.
In terms of job contract types, over 70 per cent of those employed are in permanent positions, 18 per cent are on fixed-term contracts and about 12 per cent work as casuals. The women in the sample were significantly more likely to be employed in fixed-term and casual positions. Correspondingly, the proportion of men in permanent employment is significantly higher than that of women. Lastly, there is some evidence of occupational segregation in the sample, with men heavily concentrated in the construction, mining and transport industries, and women heavily concentrated in education/training and health care industries. This is not at all surprising, except when noting that the education and health care industries comprise 39 per cent of the total workforce in the sample while the top three male-dominated industries comprise less than 6 per cent of the total workforce.
Figure 1: Gender pay gaps, mean and median incomes

Source: Author’s calculation from HILDA sample.
Large disparities in pay between men and women are also evident in the sample. For a formal measure, we analyse trends in the gender pay gap, GPG, defined as:
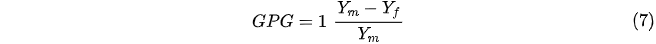
where Ym and Yf denote male and female incomes, respectively. We calculate GPG using mean and median incomes and graph the points over time in Figure 1. In terms of mean incomes, the income gap between men and women in this sample is about 35 per cent. The pay gap grew by about 5 per cent each year between 2002 and 2012, when it peaked at 40 per cent. The gap has declined since and stood at 34 per cent in 2018. The median income GPG curve is seen to rise and fall in similar magnitudes as the mean income GPG curve, although the median wage curve sat consistently lower than the mean wage curve by about 10 percentage points all through the study period. It is interesting to note that the pay gap between men and women in Australia rapidly rose during the mining boom years of 2002 and 2012 and appears to have settled to a new high in the years after that. The wage gap did not seem to be affected by the economic shocks experienced due to the global financial crisis (2007–2008). Similar trends can be seen in the wage gap calculated using median incomes.
Table 2. Quintile distribution using SEIFA Index
| Male | Female | All | ||||
| Quintile | No | % Share | No | % Share | No | % Share |
| Quintile 1 (lowest) | 421 | 8.5 | 723 | 9.8 | 1144 | 9.3 |
| Quintile 2 | 576 | 11.7 | 1017 | 13.8 | 1593 | 13.0 |
| Quintile 3 | 695 | 14.1 | 1295 | 17.6 | 1990 | 16.2 |
| Quintile 4 | 1259 | 25.5 | 1809 | 24.6 | 3068 | 25.0 |
| Quintile 5 | 1981 | 40.2 | 2508 | 34.1 | 4489 | 36.5 |
The distribution of the sample across the income quintile is shown in Table 2. Given that this cohort of individuals are all tertiary-educated, the distribution is highly skewed towards the left. The top 20 per cent account for over 36 per cent of total income, while the poorest 20 per cent account for less than 20 per cent of the total income pool. A higher share of men in the top two quintiles is also evident and a higher share of women relative to men is observed in the lowest and middle-income quintiles.
Footnotes
[1] All persons are aged 25 to 59 in CY2018, but 17 is the youngest age a person is observed in the sample.
[2] Using definitions by the Australian Bureau of Statistics.
5. Estimation of KM survival rates
This section presents estimates of the Kaplan-Meier (KM) survival probabilities for various cohort groups in the analytical sample.
Recall that KM estimates measure the fraction of subjects who survive an event for a certain amount of survival time t. In our case, the spell of interest is the period of unemployment, and, in the initial case, we are modelling the time it takes for individuals to find a full-time job after obtaining their tertiary degree.
Figure 2 and Figure 3 present the KM survival probabilities curve for the total sample population and for gender groups, respectively. The y-axis refers to the probabilities of surviving the unemployment spell, S(t), and the x-axis represents the years after completion of their tertiary qualification. In Figure 2, the survival curve is a downward sloping step function, where the rate of decrease is largest in the earliest period and gradually tapers off over time. This shape conforms to what we would normally expect of new graduates who, due to their inexperience, face significant hurdles as they enter the labour market in search of full-time jobs. Often, new graduates take on internships, traineeships, or fixed period graduate positions after graduation – many take temporary part-time jobs and/or continue to study until they secure full-time jobs. These temporary arrangements can continue for a period of time, but can provide new graduates the essential marketplace experience that can improve their practical skills and increase their chances of landing a full-time job. The KM analysis indicates these improving chances through these survival probabilities: fresh graduates have a 41 per cent chance of ‘surviving’ unemployment or remaining unemployed in the first year following graduation, falling to 27 per cent in the second year, then to 20 per cent in the third year and so on.1 These survival probabilities and the associated survival curve will serve as our benchmark as we move on and undertake analysis using a gendered approach.
Figure 2: K-M survival probabilities, all people
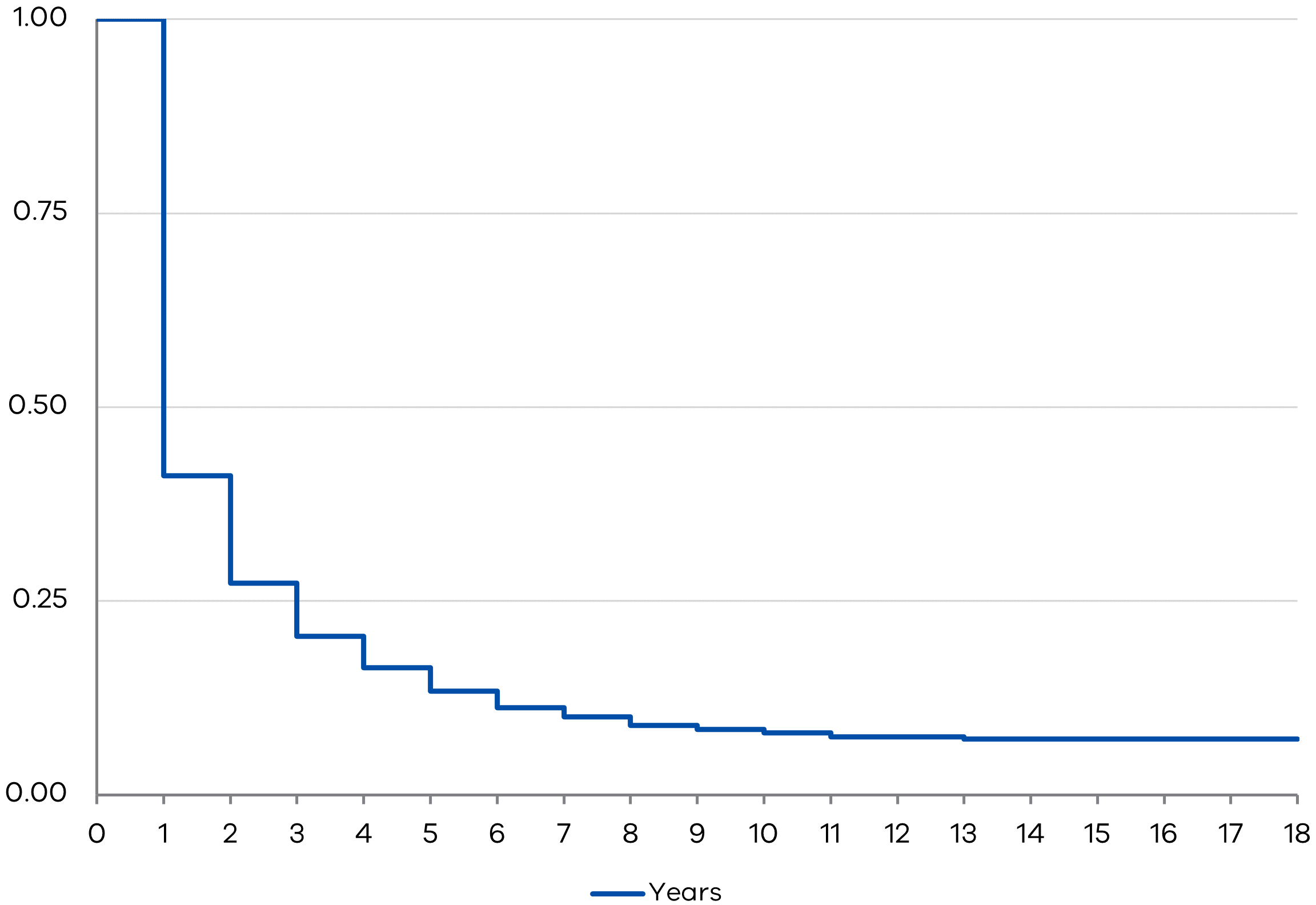
Figure 3: Survival estimates by gender
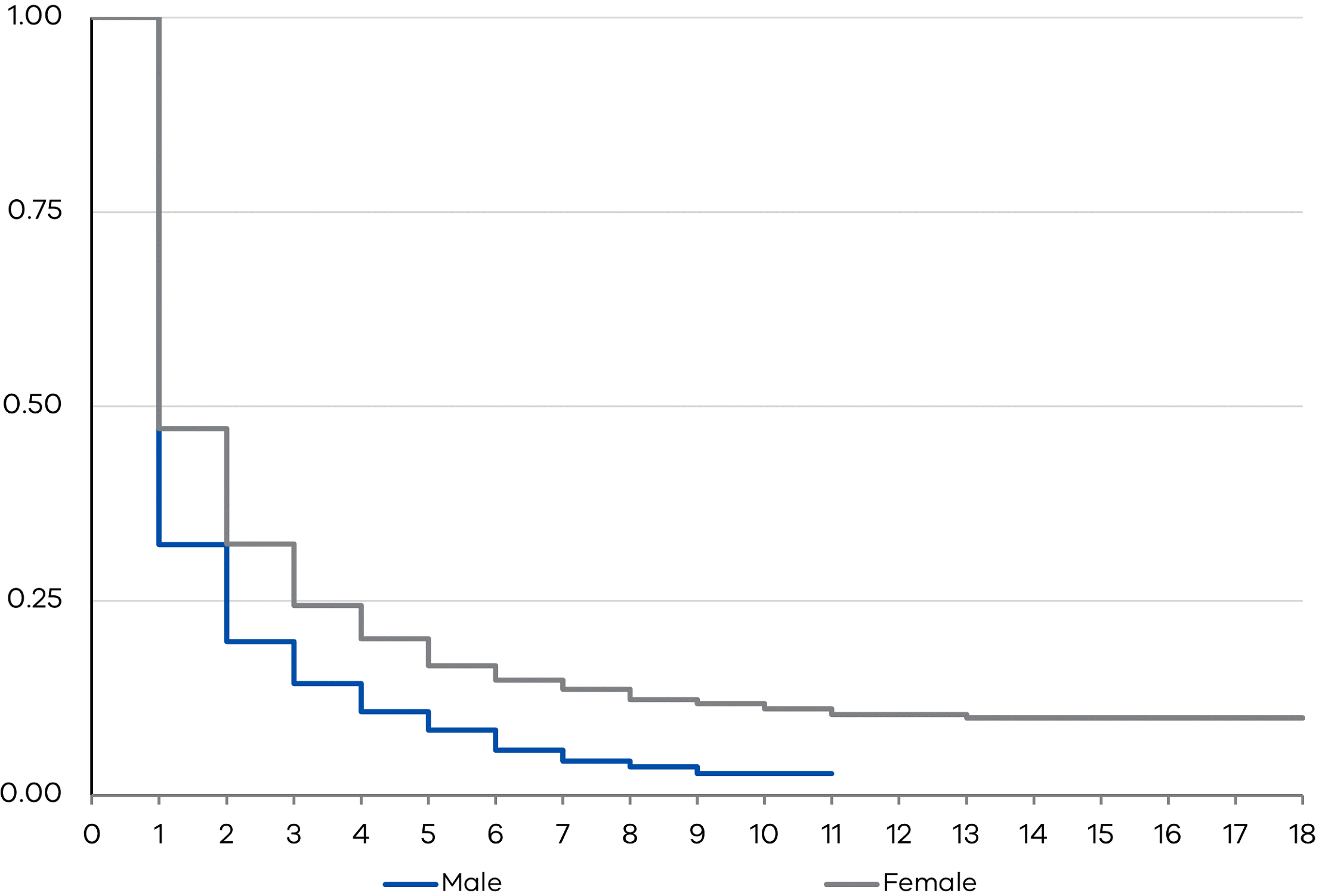
Figure 3 presents the KM survival curves for men and women. It is immediately evident that the curve for women (red) sits above the curve for men all through time. This indicates that women graduates have higher ‘survival’ rates at each time point. In other words, new women graduates took significantly more time landing full-time jobs compared to new men graduates. In more specific terms, new women graduates are shown to have a 47 per cent chance of staying (full-time) unemployed at the end of the first year, compared to just 32 per cent chance for new men graduates. In the second year, the chances of gaining full-time employment improves for both genders, but the survival rate differential is still very wide – 32 per cent chance of remaining unemployed for women compared to just 20 per cent chance for men. In the third year, the probability of finding a full-time job continues to improve for both groups but the gap in survival rates remains large: 24 per cent for women to just 14 per cent for men. These findings point not just to a significant gender gap in the labour market entry outcomes for new tertiary graduates, but also shows that these gaps can persist over years.
Our KM-based analysis is next applied to the sample grouped by common characteristics such as age, location, country of birth, marital status, parental status and gender. We find that age plays a different role for men and women. Figure 4 shows that among women who just completed a tertiary degree, those aged 40 and over appeared to take a longer time to find full-time employment compared to those aged under 40. In contrast, newly qualified older men appear to find full-time jobs quicker than their younger counterparts, with a gap of 16 percentage points in the first year, and nine percentage points in the second year. We also find that, given time, full-time employment probabilities for older and younger men converge, but we find no similar convergence in the employment probabilities for older and younger women.
Figure 4a: K-M survival probabilities by gender and age
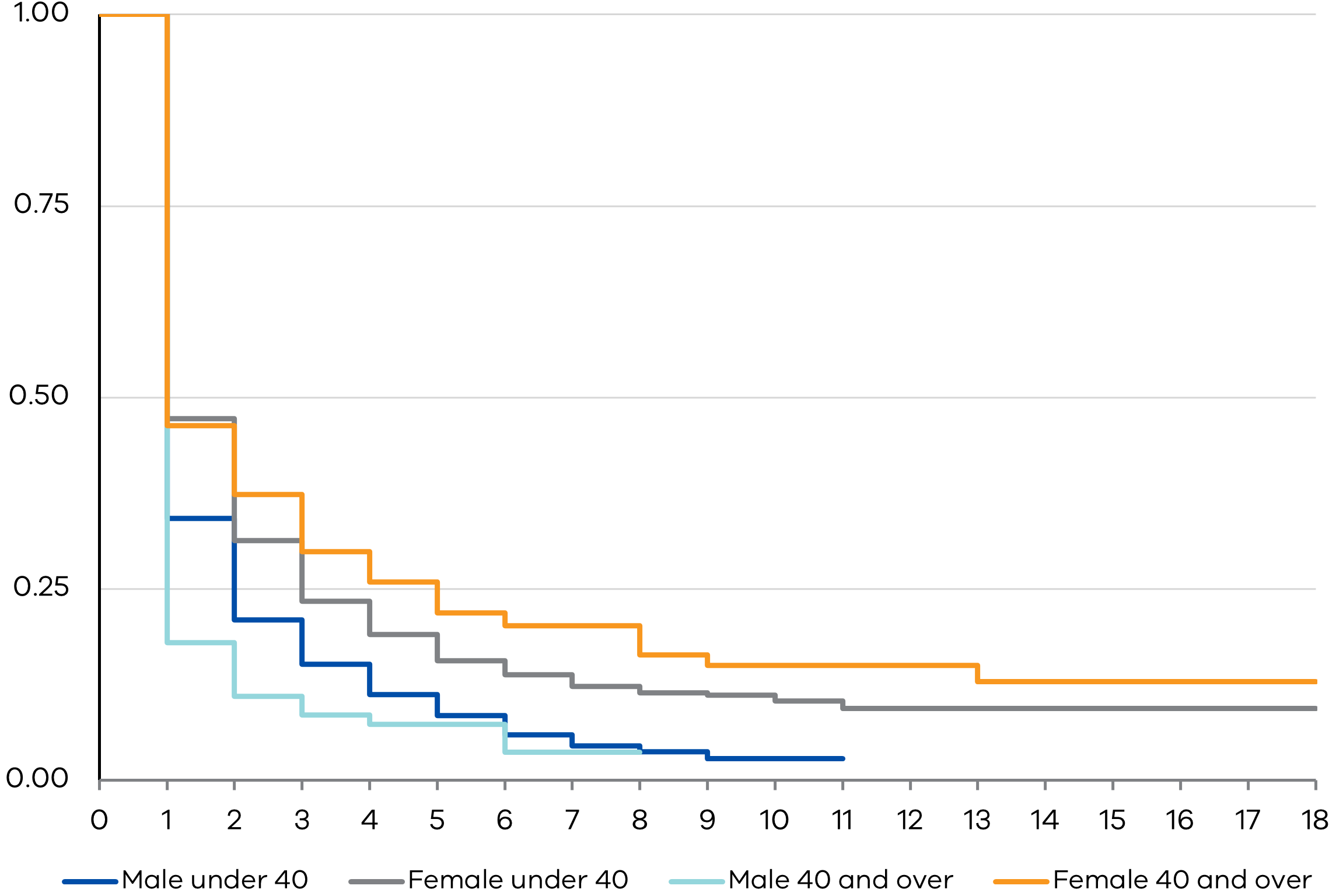
Figure 4b: K-M survival probabilities by gender and urbanity
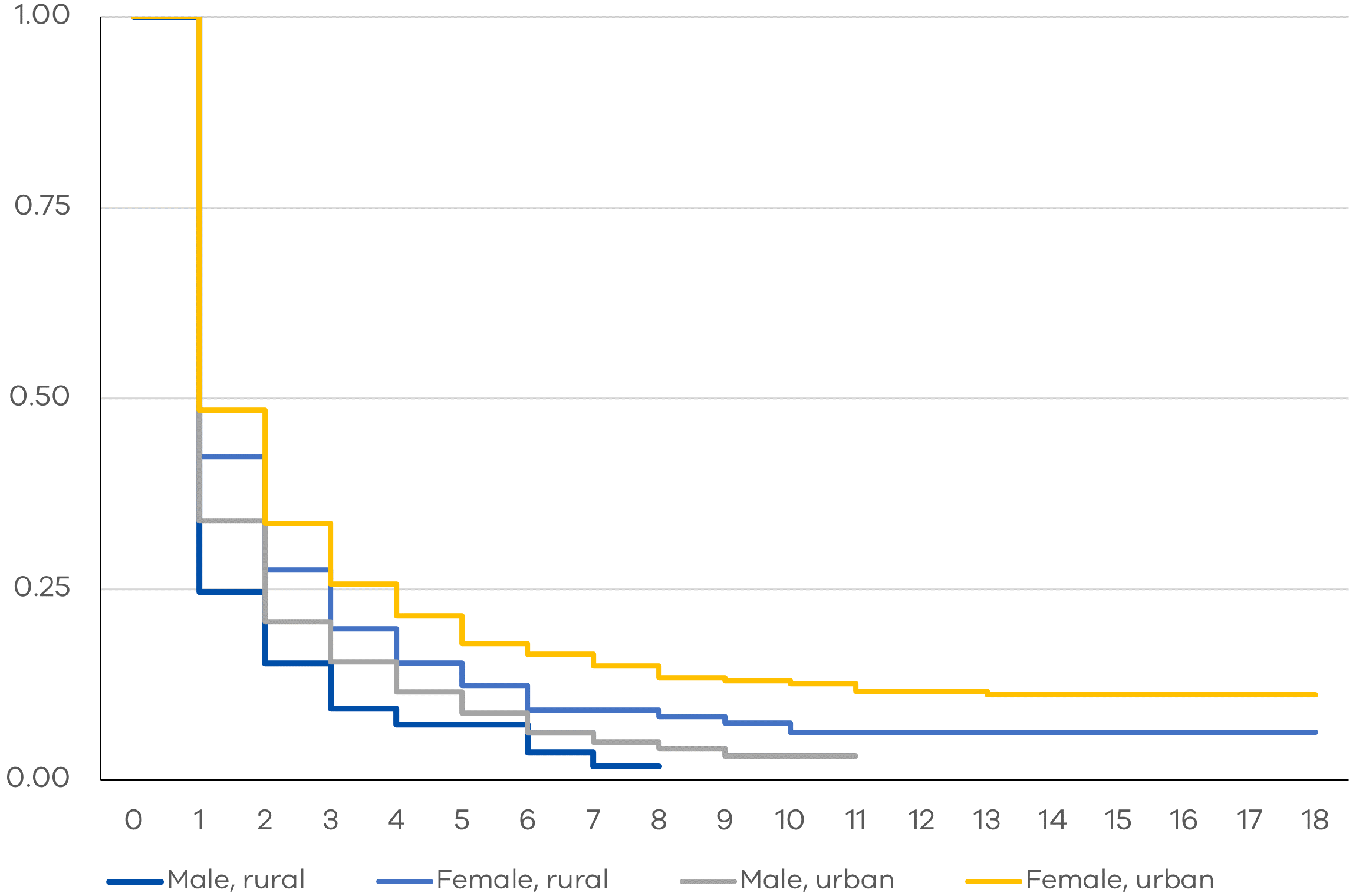
Figure 4c: K-M survival probabilities by gender and country of birth
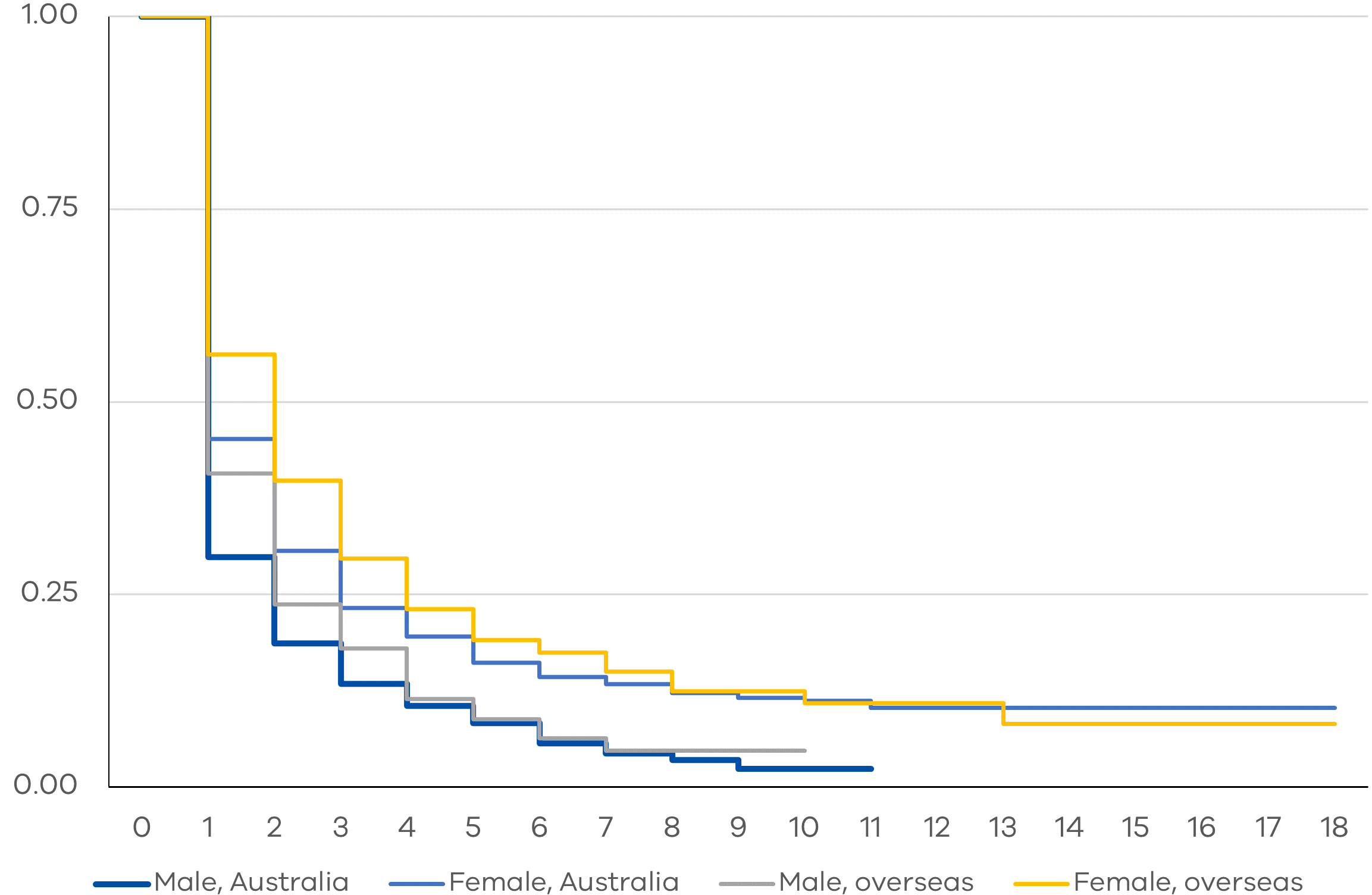
Figure 4d: K-M survival probabilities by gender and parental status
With regard to location or urbanity, we find that women living in cities take longer to find full-time jobs compared to their counterparts living in more regional areas. Given that knowledge roles are known to be concentrated in cities, it is highly probable that greater competition for high-skilled jobs in cities is driving this trend. It may also be possible that because of more limited employment opportunities for tertiary-educated individuals in regional areas, women are more likely to take on lower-skill paid employment in these locations. Among men in our sample, those living in rural areas tend to exit the unemployment queue at a faster rate than men in urban areas. Regardless of location, men experience shorter periods of unemployment than women.
With regards to country of birth, our results show trends that are consistent with the migrant assimilation story. For both men and women, we find that tertiary-educated migrants tend to stay in the unemployment queue longer than their Australian-born counterparts. However, this gap disappears over time as migrants assimilate culturally and professionally. With regards to marital status, we find that married women tend to have the longest unemployment duration spells among those looking for work while married men tend to have the shortest spells. The survival curves for single men and women do not differ significantly. We also find that KM curves for married and single women widen over time.
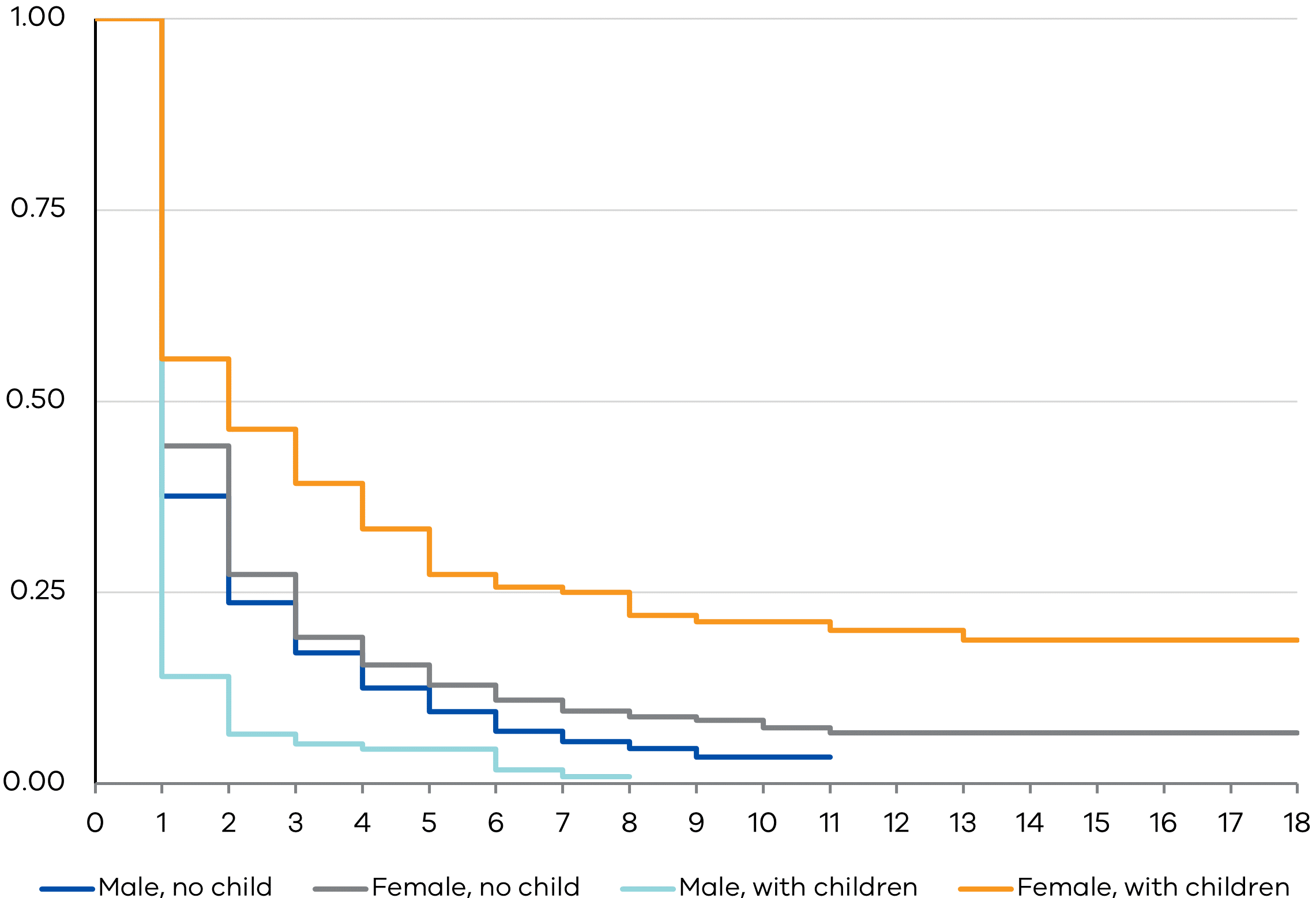
In Figure 5, the survival probabilities are calculated to obtain the KM survival curves and this time, we partition our sample into the following four groups – (i) men with children (ii) men without children (iii) women with children and (iv) women without children. As previously seen, tertiary-educated women take longer to find full-time jobs than men. Further, among women, the survival rates clearly differ between those with and without children, and that this disparity has only increased over time. The reverse is true of tertiary-educated men – men with children are found to exit the unemployment queue much quicker than men who are not parents. It is also curious to see that the survival curves for childless men and childless women do not exhibit any significant difference. Overall, the survival probability graphs appear largest between those with and without children, other things the same.
Figure 5: K-M survival probabilities by gender and marital status

Footnotes
[1] Recall that in this study, a larger ‘survival’ rate Pr(S) indicates longer times in unemployment, a negative event. Readers may find it easier to interpret this number in terms of its corresponding ‘failure’ rate Pr(F) which is a desirable event, that is, probability of finding a full-time job. Note that Pr(F) = 1 − Pr(S) where 0 < Pr(F) < 1 and 0 < Pr(S) < 1. For any cohort group therefore, we want Pr(S), to be as low as possible and Pr(F) to be as high as possible.
6. The Cox Proportional Hazard regression model: Results and discussion
In this section, we discuss results from survival analysis using the Cox Proportional Hazard modelling approach.
The KM analysis in the last section indicated trends that strongly associate particular groups with certain observed labour market outcomes, but the approach is limited in its ability to determine causation. In this section, we discuss results from survival analysis using the Cox Proportional Hazard modelling approach to identify causal factors and determine the extent of their impacts on a range of labour market outcomes with measurable degrees of confidence. In all the models we considered, the duration spell we wish to analyse is the time spent in unemployment after graduation, while the exit event (outcome) varies with each model. The spell is our dependent variable y and is fixed across the models, and our x regressor variables change with the models. To proceed, we test the impact of a set of regressors on four types of labour market outcomes – three of which are objective outcomes, and one is a subjective wellbeing measure. For the objective analysis, we use HILDA person-level data on the type of employment, level of earnings, field of education and job type. For the subjective well-being analysis, we use HILDA information on self-reported feelings of job and satisfaction measures. Further, for each model presented, three sets of results are discussed – one obtained using all people in the sample that includes a gender variable called female and two others obtained by stratifying the sample into all male and all female and estimating the models for each group.
To facilitate the discussion and understanding, it will be good to recall that the estimated coefficients pertain to the hazard ratios h(t) between a reference group r and the group of interest z, where these measure the relative speed of exiting unemployment. It will thus be very helpful to know which is the reference group. Further, in considering the numerical estimates, the following rule of thumb applies: If h(t) < 1, this means that z has a lower hazard rate compared to r, or equivalently, z has a longer median survival than r. Conversely, if h(t) > 1, this means that z has a higher valued hazard rate compared to r, or equivalently, z has a shorter median survival than r.
In Model 1 of Table 3, col (1) shows that on average, women graduates find full-time jobs 26 per cent slower than men graduates. This is about three months longer relative to the reference male who finds full-time employment within 12 months of graduation. Further, this model shows that (i) parents spend 25 per cent longer (or three months more in a year); in unemployment after graduation than their childless counterparts; (ii) those living in urban areas take 15 per cent longer (or two months more in a year) to find full-time jobs than those living in regional areas; (iii) migrants from non-English speaking countries take 16 per cent longer (or two months more in a year) to find full-time jobs than Australian-born graduates (iv) people living in areas with higher unemployment tend to be unemployed for longer than those living in areas with lower unemployment rates; and (v) more recent graduates take longer to find full-time employment than those who graduated in earlier years. The results further show that a person’s age, marital status, health, level of tertiary education and being born in an English speaking overseas country do not make a difference (positive nor negative) to one’s length of unemployment duration after graduation.
Table 3. Cox Proportional Hazard modelling results: Objective measures – employment and earnings models
| Variables | Model 1 – Finds full-time job | Model 2 – Finds permanent job | Model 3 – Total Earnings > Mean earnings | Model 4 – Total Earnings > Median earnings | ||||||||||||||||||||
| All | Male | Female | All | Male | Female | All | Male | Female | All | Male | Female | |||||||||||||
| Female+ | -0.260 | ** | -0.154 | *** | -0.413 | *** | -0.360 | *** | ||||||||||||||||
| (0.000) | (0.005) | (0.000) | (0.000) | |||||||||||||||||||||
| Age | 0.006 | 0.003 | 0.009 | -0.001 | 0.005 | -0.003 | 0.029 | *** | 0.025 | *** | 0.035 | *** | 0.027 | *** | 0.029 | *** | 0.029 | *** | ||||||
| (0.203) | (0.651) | (0.107) | (0.800) | (0.518) | (0.601) | (0.000) | (0.002) | (0.000) | (0.000) | (0.000) | (0.000) | |||||||||||||
| Parent+ | -0.247 | *** | 0.122 | -0.492 | *** | 0.040 | 0.143 | -0.027 | -0.168 | ** | 0.042 | -0.371 | *** | -0.218 | ** | -0.012 | -0.384 | *** | ||||||
| (0.003) | (0.352) | (0.000) | (0.643) | (0.305) | (0.810) | (0.072) | (0.771) | (0.003) | (0.015) | (0.931) | (0.001) | |||||||||||||
| Married/De Facto+ | 0.046 | 0.123 | -0.028 | -0.009 | -0.067 | -0.012 | 0.067 | 0.177 | -0.029 | 0.040 | 0.133 | -0.045 | ||||||||||||
| (0.438) | (0.235) | (0.705) | (0.879) | (0.546) | (0.874) | (0.344) | (0.138) | (0.746) | (0.554) | (0.246) | (0.593) | |||||||||||||
| Health scorea | -0.013 | -0.002 | -0.043 | -0.003 | 0.029 | -0.027 | -0.061 | ** | -0.053 | -0.091 | * | -0.073 | ** | -0.058 | -0.105 | ** | ||||||||
| (0.676) | (0.963) | (0.270) | (0.914) | (0.575) | (0.496) | (0.090) | (0.354) | (0.053) | (0.034) | (0.288) | (0.019) | |||||||||||||
| Urban+ | -0.152 | ** | -0.026 | -0.218 | *** | -0.133 | ** | -0.025 | -0.196 | ** | -0.004 | 0.078 | -0.046 | -0.009 | 0.073 | -0.050 | ||||||||
| (0.021) | (0.811) | (0.009) | (0.050) | (0.824) | (0.021) | (0.964) | (0.531) | (0.649) | (0.908) | (0.539) | (0.602) | |||||||||||||
| Highest degree: PhD/Masters++ | 0.099 | 0.083 | 0.084 | -0.006 | -0.053 | 0.004 | 0.480 | *** | 0.402 | *** | 0.530 | *** | 0.402 | *** | 0.280 | ** | 0.476 | *** | ||||||
| (0.185) | (0.482) | (0.385) | (0.944) | (0.677) | (0.971) | (0.000) | (0.003) | (0.000) | (0.000) | (0.031) | (0.000) | |||||||||||||
| Highest degree: Grad Dip/Cert++ | -0.012 | 0.106 | -0.112 | 0.162 | ** | 0.241 | * | 0.108 | 0.189 | ** | 0.333 | ** | 0.049 | 0.222 | *** | 0.272 | ** | 0.161 | ||||||
| (0.880) | (0.393) | (0.277) | (0.042) | (0.064) | (0.291) | (0.034) | (0.016) | (0.675) | (0.009) | (0.041) | (0.147) | |||||||||||||
| COB: English-speaking+++ | 0.026 | 0.040 | -0.007 | 0.021 | -0.152 | 0.122 | 0.113 | 0.043 | 0.158 | 0.100 | 0.122 | 0.072 | ||||||||||||
| (0.821) | (0.811) | (0.965) | (0.856) | (0.394) | (0.449) | (0.368) | (0.813) | (0.368) | (0.410) | (0.489) | (0.667) | |||||||||||||
| COB: Non-English speaking+++ | -0.159 | ** | -0.157 | -0.127 | -0.189 | ** | -0.256 | ** | -0.122 | -0.342 | *** | -0.304 | ** | -0.353*** | -0.356 | *** | -0.309 | ** | -0.376 | *** | ||||
| (0.040) | (0.173) | (0.228) | (0.021) | (0.039) | (0.262) | (0.000) | (0.027) | (0.007) | (0.000) | (0.019) | (0.002) | |||||||||||||
| Area unemployment rate | -0.067 | *** | -0.061 | -0.077 | ** | -0.054 | ** | -0.042 | -0.066 | * | -0.039 | -0.081 | * | 0.001 | -0.052 | * | -0.081 | * | -0.026 | |||||
| (0.010) | (0.121) | (0.027) | (0.048) | (0.315) | (0.063) | (0.208) | (0.071) | (0.984) | (0.079) | (0.063) | (0.510) | |||||||||||||
| Year of graduation | -0.016 | *** | -0.016 | * | -0.014 | ** | -0.012 | ** | -0.016 | * | -0.009 | -0.052 | *** | -0.048 | *** | -0.054*** | -0.043 | *** | -0.041 | *** | -0.044 | *** | ||
| (0.004) | (0.067) | (0.066) | (0.035) | (0.087) | (0.216) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |||||||||||||
+Binary; Base variables are male, no children, single, rural. ++ Tertiary Degree Base: Bachelors/Honours. +++Country of Birth base is Australia. aHealth Score ranges from 1 (excellent) to 5 (poor), self-rated. *Significant at the 1 per cent level **Significant at the 5 per cent level ***Significant at the 10 per cent level.
Overall, results in Model 1 provides strong empirical support for the claim that women face large labour market penalties based on their gender and parental status. The gender disaggregated results in columns (2) and (3) show that the parent variable is highly significant for women but insignificant for men, implying that being a father does not affect unemployment exit rates for men, but a high level of disadvantage is evident for mothers seeking full-time employment compared to women without children. The results also show that the impact of major city living on finding full-time employment is gendered, as women living in cities experience longer periods of unemployment than men, as well as women, in regional/rural areas. This result supports the claim that women in both inner and outer metropolitan areas are experiencing severe and entrenched disadvantage (Productivity Commission 2017).
In Model 2, the exit event is finding a permanent job. As in Model 1, we find that being a woman, living in major cities, being a migrant from a non-English speaking nation, area unemployment rate and year of graduation are significant factors holding back individuals from finding a permanent job. The associated coefficients’ signs are also all found to be negative and gendered, indicating higher wage penalties accruing to women than men. Unlike Model 1, however, results in Model 2 show that being a parent is not a significant factor in finding a permanent job, but that having a graduate diploma or certificate improves one’s chances of permanent employment, particularly for men. Further, we find that being a migrant from a non-English speaking country and year of graduation penalises men more than women, while living in areas where unemployment is high penalises women more than men.
In Model 3, the exit event occurs when the individual’s annual earnings start to exceed the average earnings of everyone in the sample. Here, we again find that gender, being a parent, a migrant from a non-English speaking nation, living in high unemployment rate areas and recent years of graduation present significant downside risks. In contrast, living in major cities appears to be of no consequence. Other demographic variables like age, health and additional tertiary qualifications now also emerge as significant regressors. The coefficients for age across the various specifications are highly significant and positive, implying that the older a person is, the quicker their earnings can rise above that of the average person and we find these results hold with larger effects across the disaggregated men and women regressions. Health also becomes important in this model, with the model showing that poorer health causes a relatively slow progression to above-average levels of earnings, and that this effect is more pronounced for women compared to men. The two education variables are also found to be highly significant in influencing this earnings outcome. The PhD/masters and grad dip/cert variables are both significant and positive, meaning that people with these extra qualifications achieve this benchmark earnings quicker than those without them. Model 4 is a slight modification to Model 3 in that we benchmark total earnings with median, rather than mean, earnings. The results for this model are very similar to those of Model 3.
We now discuss our job-skills match models in Table 4, which examine the role of occupation type in the graduate labour market. To identify a job-skills mismatch in this article, we use the job analysis method used in McDonald and Valenzuela (2017). The educational requirements of the person’s occupation are ranked and compared to their educational qualifications, and a mismatch is identified if the former is less than the latter. In determining the educational requirements of particular occupations, guidance is taken from the Occupation ANZCO 2006 system which, at its broadest level, identifies four broad occupation skill levels and the educational qualifications required for each. In our sample, a match occurs if they are either a manager or a professional. Anything coded 2 or higher in the ANZCO value label is considered a mismatch and a higher value indicates a higher degree of occupational mismatching.
Table 4. Cox Proportional Hazard Modelling Results: Objective Measures - Job Skill Match Models
| Model 5 – Job-skill match | Model 6 – Total earnings > mean earnings | Model 7 – Total earnings > median earnings | ||||||||||||||||
| Variables | All | Male | Female | All | Male | Female | All | Male | Female | |||||||||
Female+ | -0.015 | * | -0.434 | *** | -0.372 | *** | ||||||||||||
| (0.776) | (0.000) | (0.000) | ||||||||||||||||
| Age | 0.006 | -0.003 | 0.013 | ** | 0.027 | *** | 0.024 | *** | 0.031 | *** | 0.025 | *** | 0.029 | *** | 0.024 | *** | ||
| (0.200) | (0.660) | (0.027) | (0.000) | (0.004) | (0.000) | (0.000) | (0.001) | (0.000) | ||||||||||
| Parent+ | -0.099 | 0.079 | -0.221 | ** | -0.139 | -0.016 | -0.296 | ** | -0.176 | * | -0.078 | -0.280 | ** | |||||
| (0.238) | (0.564) | (0.040) | (0.156) | (0.915) | (0.029) | (0.064) | (0.590) | (0.030) | ||||||||||
| Married/de facto+ | 0.152 | ** | 0.099 | 0.187 | ** | 0.023 | 0.109 | -0.051 | -0.022 | 0.029 | -0.080 | |||||||
| (0.012) | (0.363) | (0.012) | (0.759) | (0.384) | (0.591) | (0.752) | (0.807) | (0.373) | ||||||||||
| Health scorea | -0.023 | -0.010 | -0.030 | -0.030 | -0.017 | -0.053 | -0.045 | -0.003 | -0.085 | * | ||||||||
| (0.460) | (0.841) | (0.442) | (0.438) | (0.783) | (0.289) | (0.219) | (0.966) | (0.078) | ||||||||||
| Urban+ | -0.164 | ** | -0.093 | -0.205 | ** | 0.062 | 0.065 | 0.058 | 0.069 | 0.081 | 0.063 | |||||||
| (0.013) | (0.402) | (0.013) | (0.442) | (0.605) | (0.588) | (0.371) | (0.503) | (0.535) | ||||||||||
| Highest degree: PhD/Masters++ | 0.305 | *** | 0.364 | *** | 0.273 | *** | 0.415 | *** | 0.356 | ** | 0.452 | *** | 0.353 | *** | 0.275 | ** | 0.397 | *** |
| (0.000) | (0.003) | (0.004) | (0.000) | (0.011) | (0.000) | (0.000) | (0.044) | (0.000) | ||||||||||
| Highest degree: Grad Dip/Cert++ | 0.145 | * | 0.225 | * | 0.087 | 0.117 | 0.196 | 0.024 | 0.171 | ** | 0.172 | 0.155 | ||||||
| (0.063) | (0.085) | (0.378) | (0.205) | (0.165) | (0.850) | (0.053) | (0.207) | (0.188) | ||||||||||
| Job-skill mismatch score(b) | -0.292 | *** | -0.289 | *** | -0.293 | *** | -0.284 | *** | -0.272 | *** | -0.300 | *** | ||||||
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |||||||||||||
| COB: English-speaking+++ | 0.190* | 0.291* | 0.103 | 0.030 | -0.099 | 0.160 | 0.044 | 0.001 | 0.096 | |||||||||
| (0.088) | (0.087) | (0.489) | (0.819) | (0.598) | (0.392) | (0.725) | (0.997) | (0.590) | ||||||||||
| COB: Non-English speaking+++ | -0.321 | *** | -0.234 | * | -0.379 | *** | -0.235 | ** | -0.154 | -0.283 | * | -0.252 | ** | -0.188 | -0.275 | ** | ||
| (0.000) | (0.062) | (0.001) | (0.025) | (0.290) | (0.062) | (0.011) | (0.179) | (0.051) | ||||||||||
| Area unemployment rate | -0.032 | -0.043 | -0.023 | -0.027 | -0.065 | 0.004 | -0.040 | -0.065 | -0.022 | |||||||||
| (0.217) | (0.296) | (0.496) | (0.405) | (0.168) | (0.931) | (0.198) | (0.158) | (0.598) | ||||||||||
| Year of graduation | -0.016 | * | -0.020 | ** | -0.012 | * | -0.051 | *** | -0.044 | *** | -0.056 | *** | -0.040 | *** | -0.034 | *** | -0.044 | *** |
| (0.004) | (0.024) | (0.092) | (0.000) | (0.000) | (0.000) | (0.000) | (0.001) | (0.000) | ||||||||||
+Binary; Base variables are male, no children, single, rural, ++ Tertiary Degree Base: Bachelors/Honours. +++Country of Birth base is Australia. aHealth Score ranges from 1 (excellent) to 5 (poor), self-rated. bjob mismatch score ranges from 1 (match) to 4 (greatest mismatch). *Significant at the 1 per cent level **Significant at the 5 per cent level ***Significant at the 10 per cent level.
In Model 5, our exit variable is finding a job that matches the person’s qualification. Here, we find that gender, marital status, living in major cities, additional degrees, being a migrant and year of graduation are important determinants of labour market outcomes. The gender coefficient is significant and negative, implying that relative to men, women take longer to find a job that matches their tertiary qualifications. Marital status is not significant for men but highly significant for women. Age is not significant overall but becomes significant if the regression is restricted to women only. The same holds for the parent variable – it is not significant overall, but becomes significant in the women-only regressions, indicating lengthier spells for achieving a job-skill match for mothers than for fathers. In Models 6 and 7, the exit events are defined by achieving above-average mean and median earnings, respectively, and the job-skill match identifier is made a covariate rather than a dependent variable, as was done in Model 5. Here, we find that this job-skill variable is highly significant in both models, meaning that the greater degree of mismatch one experiences on the job, the longer it takes to achieve mean or median earnings level, which makes perfect sense. For the other covariates, we find that being a parent, health and being a migrant from a non-English speaking country can cause longer durations for women than men in this model, while the other significant covariates are non-gendered.
Lastly, we discuss Table 5, which presents the results from our subjective hazard rate models. These models are deemed subjective because the exit events are based on self-rated survey responses using feelings or impressions. In particular, the key survey responses we use are ‘I feel secure in my current job’ (Model 8) and ‘I use my skills in my current job’ (Model 9). The modelling exercise returned weaker effects compared to the more objective models presented earlier. For example, in Model 8, we find that health is very important in feeling secure in the job for both men and women, while a non-English language background matters more for men and area unemployment rate matters more for women. For Model 9, we find that having a non-English language background is highly significant for women only and that an additional graduate qualification (diploma or certificate) matters to men’s occupation-skill match impressions.
Table 5. Cox Proportional Hazard modelling results: Subjective measures
Variables | Model 8 – I feel secure in my current job | Model 9 – I use my skills in my current job | ||||||||||
| All | Male | Female | All | Male | Female | |||||||
| Female+ | -0.049 | -0.023 | ||||||||||
| (0.451) | (0.649) | |||||||||||
| Age | 0.001 | -0.008 | 0.008 | 0.005 | -0.003 | 0.009 | ||||||
| (0.870) | (0.380) | (0.263) | (0.297) | (0.700) | (0.102) | |||||||
| Parent+ | 0.019 | 0.216 | -0.142 | -0.043 | 0.099 | -0.134 | ||||||
| (0.845) | (0.168) | (0.278) | (0.589) | (0.455) | (0.188) | |||||||
| Married/De Facto+ | 0.114 | 0.103 | 0.110 | 0.053 | 0.031 | 0.066 | ||||||
| (0.121) | (0.430) | (0.223) | (0.357) | (0.767) | (0.351) | |||||||
| Health Scorea | -0.100 | *** | -0.118 | ** | -0.095 | ** | -0.035 | -0.068 | -0.023 | |||
| (0.009) | (0.067) | (0.048) | (0.235) | (0.170) | (0.533) | |||||||
| Urban+ | -0.084 | -0.147 | -0.055 | -0.113 | * | -0.136 | -0.110 | |||||
| (0.287) | (0.246) | (0.588) | (0.075) | (0.198) | (0.167) | |||||||
| Highest degree: PhD/Masters++ | 0.045 | 0.118 | -0.017 | 0.091 | 0.193 | 0.045 | ||||||
| (0.622) | (0.427) | (0.884) | (0.206) | (0.108) | (0.621) | |||||||
| Highest degree: Grad Dip/Cert++ | 0.116 | 0.210 | 0.046 | 0.124 | * | 0.268 | ** | 0.049 | ||||
| (0.209) | (0.161) | (0.698) | (0.099) | (0.035) | (0.602) | |||||||
| COB: English-speaking+++ | 0.065 | 0.037 | 0.079 | 0.075 | 0.144 | 0.019 | ||||||
| (0.626) | (0.854) | (0.655) | (0.492) | (0.389) | (0.896) | |||||||
| COB: Non-English speaking+++ | -0.363 | *** | -0.542 | *** | -0.218 | -0.222 | *** | -0.152 | -0.263 | *** | ||
| (0.001) | (0.002) | (0.112) | (0.004) | (0.195) | (0.009) | |||||||
| Area unemployment rate | -0.070 | ** | -0.043 | -0.091 | ** | -0.037 | -0.026 | -0.046 | ||||
| (0.026) | (0.373) | (0.029) | (0.148) | (0.504) | (0.163) | |||||||
| Year of graduation | -0.008 | -0.008 | -0.007 | -0.005 | -0.004 | -0.004 | ||||||
| (0.218) | (0.433) | (0.425) | (0.357) | (0.609) | (0.531) | |||||||
+Binary; Base variables are male, no children, single, rural. ++ Tertiary Degree Base: Bachelors/Honours. +++Country of Birth base is Australia. aHealth Score ranges from 1 (excellent) to 5 (poor), self-rated.
7. Discussion of results
This section presents the results from this research paper.
The results presented in the preceding section confirm that there are large differences in labour market outcomes between men and women in the Australian graduate labour market, despite the economy’s success in closing the education gap between these two groups in the workforce. In particular, our results show that women take longer to find full-time employment after tertiary level graduation and to achieve important benchmarks in the labour market such as finding permanent jobs, finding jobs that match their area of tertiary training, achieving above-average earnings and feeling secure in the job that they currently have. Our semi-parametric duration analysis identifies several confounding factors. Being a parent, being a migrant from a non-English speaking nation, living in major cities, living in areas with a high unemployment rate and year of graduation are each found to exert significant negative influences on employment outcomes generally, but more acutely for women. Most notable of these is the parent factor for women – motherhood appears consistently as the main cause of lengthy delays (of as much as six months) for women in reaching important milestones in the labour market. In contrast, our results also showed that being a parent is inconsequential for men’s labour market outcomes – that is, fatherhood neither improves nor worsens men’s ability to find full-time, permanent employment, or to achieve above average earnings or feel secure in the jobs they currently have.
These results make intuitive sense given traditional gender roles in typical Australian household – that is, women continue to take the larger share of unpaid household and care work, while men are relied on as main breadwinners and thus continue to spend longer hours in paid work (Baxter and Hewitt 2013; Craig and Brown 2017; Craig and Churchill 2021). We however need to qualify these results because of selection bias and other unobserved factors that could not be accounted for. Selection bias in labour force studies arises because data on wages and related outcomes are available only for a self selected group of labour force participants. This data inherently rests on the individuals’ decisions on whether or not to participate in the labour force, which are in turn determined by one’s tastes, preferences, work and family values, sense of competitiveness and/or attitudes to risk (Stam et.al. 2014; Blau and Kahn 2017, Mitri 2021) all of which are unobserved.1 It is thus highly possible that we have not accounted for the roles that these unobservable variables may have had on the estimated survival rates and therefore our findings should be interpreted with caution.2
That said, some aspects of this study can support a strong causal effect narrative. First, our sample is relatively homogenous and limited to the highly educated. Second, we use longitudinal data and duration modelling techniques. On the first point, we can draw from the findings of Noonan et al. (2005) and Bertrand et al. (2010) in their analysis of observed wage gaps among lawyers and MBA graduates, respectively. Using samples of highly educated men and women, both studies conclusively found that considerable portions of observed gender differences can be explained by labour supply factors like weekly hours and actual post-qualification work experience, which were in turn related to career-family trade-offs. On the second point, we draw on the linked data labour literature – notably the work of Hirsch et al (2010) and Ludsteck (2014), which uses longitudinal linked data and an individual fixed effects approach to address the selection issues. Both articles provide clear empirical evidence confirming that observed wage penalties for women are strongly associated with observed worker and job characteristics. Lastly, we draw on the specialisation-in-the-family argument first raised in Becker (1991). Accordingly, traditional notions of gender roles that view the husband as the primary earner may increase married men’s effort and motivation, and hence improve their labour market outcomes much faster than married women. Overall, the empirical evidence suggests that some portion of the observed relationship between gender and time needed to achieve outcomes in the labour market is causal.
On education, our gender-differentiated regressions show that completing a higher degree certificate or diploma hastens men’s ability to land permanent jobs and achieve above average earnings, while this extra qualification does not make any difference for women’s outcomes. This speaks to the issue of return on investment in higher education, regardless of whether this cost is borne by the government (via scholarships, financial incentives etc.) or by the individual. The immediate implication is that it is more worthwhile for men to study more and qualify for a minor, year-long second tertiary degree, as data shows such investment fast-tracks their career progression after employment. For women, on the other hand, investment in further education does not seem pay career dividends until the qualification pursued is at the highest levels (a masters or PhD degree).
Given that our sample consists of tertiary qualified men and women, our results are consistent with the finding that gender gaps are much slower to close among the highly skilled workforce than the general workforce (Arulampalam et al. 2007; Albrecht, Björklund, and Vroman 2003; Blau and Kahn 2017). For the case, our findings could reflect several possible factors in the Australian labour market that disadvantage women, including the presence of gender discrimination and the existence of a glass ceiling effect. Alternatively, it may also be that such findings result from other unmeasured factors that could lead men and women on the top of the distribution to behave differently. These possibilities will be explored in an extension paper that will investigate in far greater detail the role of higher education, alongside occupation and industry, in accounting for observed gender gaps, and how these variables interact with parenthood and the other relevant covariates.
Interestingly, we also find two other variables that appear to hold back women from achieving employment benchmarks in good time: living in major cities (as opposed to regional centres) and living in areas of high unemployment. For the first case, given higher rates of competition for full-time permanent jobs in large cities, it may be that women’s higher risk aversion profile cause them to accept less than ideal job offers too quickly, as seen in Cortes et. al (2021), which can then prolong the time it takes to land more permanent, full-time jobs that better match their skills. Bertrand (2018) however offers empirical evidence indicating that only 10 to 15 per cent of differences in labour market outcomes are due to psychological attributes such as risk aversion, confidence or competitiveness. Rather, Bertrand (2018) highlights that women have a relatively higher demand on their time outside the labour market (such as in childcare and other forms of nonmarket work), which then leads them to hold stricter conditions of jobs acceptance. These conditions may include more flexible or part-time work, which is harder to find in large cities where there is greater competition. Additionally, these demands on their time can give women less time to spend on job searching and applications. In short, women in cities may be one of those groups experiencing severe and entrenched disadvantage across both inner and outer metropolitan areas.
For job-skill match outcome, we find that age matters for women – indicating lengthier spells for achieving a job-skill match for older women than similarly aged men. On finding a permanent job, we find that being a parent is not significant, but that having a graduate diploma or certificate improves one’s chances of finding a permanent job, particularly for men. Finally, we find that individuals from non-English speaking countries and year of graduation penalises men more than women, while area unemployment rate penalises women more than men.
With regards to the covariate living in areas of high unemployment, this is thought to reflect the delicate balancing act that women have to do to pursue a successful career and attend to family caring duties at the same time. Our results are consistent with previous studies that show commuting times are a strong determinant of the labour supply in US cities (Black et al. 2014). Married women, particularly those with young children, are particularly sensitive to commuting time (Rosenthal and Strange 2012). Married women with young children located in close geographical proximity to their mothers or mothers-in-law can more easily participate in the labour market given the availability of childcare (Compton and Pollak 2014). Indeed, previous work by Le Barbanchon et al. (2019) shows that, on average, women have a lower willingness to commute relative to men.
Footnotes
[1] Possible selection bias in measuring differences in outcomes is an important and complex issue. Thus, it may not be surprising that efforts to address it have not yet achieved a consensus. Some differences arise because each of the reviewed studies not only focuses on a different data set or time period, but each uses a different approach to correcting for selection or implements it differently - including different definitions of the wage sample and different specifications of estimating equations.
[2] The economic literature is however unclear whether the issue of selection produces biased results; a comprehensive review of empirical works concludes that the evidence is mixed (Blau and Kahn 2017).
8. Conclusion
This study examines labour market outcomes between tertiary-educated men and women in Australia using duration modelling techniques.
It confirms the existence of gaps between men and women in the Australian graduate labour market and identifies a number of likely causes of their persistence over time. Our main findings suggest that compared to men, women take more time to find full-time employment after graduating with a tertiary qualification and more time to achieve important benchmarks in the labour market such as finding permanent jobs, finding jobs that match their area of tertiary training, achieving above-average earnings and feeling secure in the job that they currently have. Our results make great practical sense and are consistent with those in the labour economics literature. We nonetheless advise caution in interpreting these results.
Our results imply that traditional gender roles that oblige women to take on a greater share of unpaid and care work in the typical family home hold women back from achieving employment outcomes that are at least on par with men and from maximising their investment in human capital. Education expansion is a step in the right direction, but the data seems to show that expanding education alone is not enough to address the persistence of these gaps. A realignment of gender roles and perceptions in all corners of society – in the home, in schools and in workplaces – is needed to consolidate gains on the education front. In terms of policy, our results imply that a package of structural reforms in the labour market may be needed to complement education initiatives. We suggest that these reforms can be designed with a view to eliminate bias against women, including perceptions of lower productivity compared to men due to more family ‘caring’ duties in particular times of the life cycle.
9. References
References for this Victoria’s Economic Bulletin research article.
Albrecht J, Bjorklund A and Vroman S (2003) ‘Is there a glass ceiling in Sweden?’ Journal of Labor Economics(opens in a new window), 21(1): 145-177.
Arulampalam W, Booth A &and Bryan M (2007). ‘Is There a Glass Ceiling over Europe? Exploring the Gender Pay Gap across the Wage Distribution’. ILR Review, 60(2): 163–186.
Barón, J.D. and Cobb‐Clark, D.A., 2010. Occupational segregation and the gender wage gap in private‐and public‐sector employment: a distributional analysis. Economic Record, 86(273), pp.227-246.
Baxter J and Hewitt B (2013). ‘Negotiating Domestic Labor: Women's Earnings and Housework Time in Australia’. Feminist Economics, 19:1, 29-53.
Becker G. S. (1991). A treatise on the family: Enlarged edition. Harvard university press.
Bertrand M. (2018). ‘Coase lecture–the glass ceiling’ Economica, 85(338): 205-231.
Bertrand M, Goldin C and Katz L F 2010. "Dynamics of the Gender Gap for Young Professionals in the Financial and Corporate Sectors." American Economic Journal: Applied Economics, 2 (3): 228-55.
Borland J. (1999). ‘Earnings inequality in Australia: Changes, causes and consequences.’ Economic Record, 75(2): 177-202.
Borland J and Coelli M (2016) ‘Labour market inequality in Australia.’ Economic Record, 92(299): 517-547.
Benos N and Zotou S (2014). ‘Education and economic growth: A meta-regression analysis’ World Development, 64: 669-689.
Black D A, Kolesnikova N and Taylor L J (2014) ‘Local labor markets and the evolution of inequality’ Annu. Rev. Econ., 6(1): 605-628.
Blau F D and Kahn L M (2017). ‘The gender wage gap: Extent, trends, and explanations.’ Journal of Economic Literature, 55(3): 789-865.
Card D (2001) ‘Estimating the Return to Schooling: Progress on Some Persistent Econometric Problems’, Econometrica, 69 (5): 1127-1160.
Cobb-Clark D A and Tan M (2011). ‘Noncognitive skills, occupational attainment, and relative wages.’ Labour Economics, 18(1): 1-13.
Coelli M (2014). ‘Occupational differences and the Australian gender wage gap.’ Australian Economic Review, 47(1): 44-62.
Coelli M and Borland J (2016). ‘Job polarisation and earnings inequality in Australia.’ Economic Record, 92(296): 1-27.
Compton J and Pollak R A (2014). Family proximity, childcare, and women’s labor force attachment. Journal of Urban Economics, 79, 72-90.
Conti G, Heckman J and Urzua S (2010). ‘The education-health gradient.’ American Economic Review, 100(2), 234-38.
Cortés P, Pan J, Pilossoph L and Zafar B (2021). ‘Gender differences in job search and the earnings gap: Evidence from business majors.’ (No. w28820). National Bureau of Economic Research.
Craig L and Brown J E (2017). ‘Feeling rushed: Gendered time quality, work hours, nonstandard work schedules, and spousal crossover.’ Journal of Marriage and Family, 79(1), 225-242.
Craig L and Churchill B (2021). ‘Working and caring at home: Gender differences in the effects of COVID-19 on paid and unpaid labor in Australia.’ Feminist economics, 27(1-2), 310-326.
Farber H S.(opens in a new window)(2004), "JOB LOSS IN THE UNITED STATES, 1981–2001", Polachek, S.W.(opens in a new window) (Ed.) Accounting for Worker Well-Being (Research in Labor Economics, Vol. 23), Emerald Group Publishing Limited, Bingley, pp. 69-117.
Guo, S. (2010). Survival analysis. Oxford University Press.
Gokulsing D and Tandrayen-Ragoobur, V. (2014). ‘Gender, education and labour market: Evidence from Mauritius’. International Journal of Sociology and Social Policy.
Hirsch B, Schank T and Schnabel C. (2010). ‘Differences in labor supply to monopsonistic firms and the gender pay gap: An empirical analysis using linked employer-employee data from Germany’. Journal of Labor Economics 28(2): 291–330.
ILO 2022. The gender gap in employment: What's holding women back?
https://www.ilo.org/infostories/en-GB/Stories/Employment/barriers-women…(opens in a new window)
Kaplan E L and Meier P (1958). ‘Nonparametric estimation from incomplete observations.’ Journal of the American statistical association, 53(282): 457-481.
Kee H. J. (2006). ‘Glass ceiling or sticky floor? Exploring the Australian gender pay gap.’ Economic Record, 82(259): 408-427.
Klasen S (2018). ‘The impact of gender inequality on economic performance in developing countries.’ Annual Review of Resource Economics, 10: 279-298.
Lagerlöf N P (2003). ‘Gender equality and long-run growth.’ Journal of Economic Growth, 8(4): 403-426.
Le Barbanchon T, Rathelot R and Roulet A (2019). ‘Unemployment insurance and reservation wages: Evidence from administrative data.’ Journal of Public Economics, 171: 1-17.
Ludsteck J. (2014). ‘The Impact of Segregation and Sorting on the Gender Wage Gap: Evidence from German Linked Longitudinal Employer-Employee Data’. ILR Review. 67(2):362-394.
Machin S, Marie O, and Vujić S. (2011). ‘The crime reducing effect of education.’ The Economic Journal, 121(552): 463-484.
Miller P W (2005). ‘The role of gender among low-paid and high-paid workers.’ Australian Economic Review, 38:405–417
Mitri K (2021). ‘Does higher education make a difference? The influence of educational attainment on women's and men's nonstandard employment outcomes.’ Canadian Review of Sociology/Revue canadienne de sociologie, 58(1): 25-44.
McDonald J T, and Valenzuela M R (2017). ‘How does skills mismatch affect remittances? A study of Filipino migrant workers.’ Contemporary Economic Policy, 35(1): 216-231.
Miller P W (1994). ‘Gender discrimination in training: An Australian perspective.’ British Journal of Industrial Relations, 32(4):539-564.
Nica M (2019). ‘The relationship between self-employment and economic development.’ Southwestern Economic Review, 46: 59-85.
Nickell S (1979). ‘Education and lifetime patterns of unemployment.’ Journal of Political Economy, 87(5, Part 2): S117-S131.
Nguyen C P (2021). ‘Gender equality and economic complexity.’ Economic Systems, 45(4), 100921.
Noonan M C, Corcoran M E and Courant P N, Pay Differences Among the Highly Trained: Cohort Differences in the Sex Gap in Lawyers' Earnings, Social Forces, Volume 84, Issue 2, December 2005, Pages 853–872.
Oreopoulos P and Salvanes K G (2009). ‘How large are returns to schooling? Hint: Money isn't everything’ (No. w15339). National Bureau of Economic Research.
Productivity Commission 2017, Transitioning Regional Economies, Study Report, Canberra.
Rosenthal S and Strange W C (2012). ‘Female entrepreneurship, agglomeration, and a new spatial mismatch.’ Review of Economics and Statistics, 94(3): 764-788.
Stam K, Verbakel E and de Graaf P M (2014). ‘Do values matter? The impact of work ethic and traditional gender role values on female labour market supply.’ Social indicators research, 116(2): 593-610.
Theodossiou I and Zangelidis A (2009).’ Should I stay or should I go? The effect of gender, education and unemployment on labour market transitions.’ Labour Economics, 16(5): 566-577.
Wooden, M. (1999). ‘The employment consequences of comparable worth policies.’ The Australian Economic Review, 32(3): 286-291.
World Economic Forum, The Global Gender Gap Report 2020, 2021.

