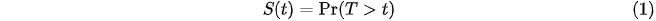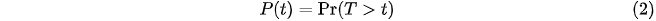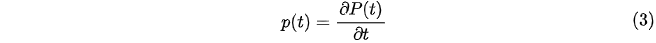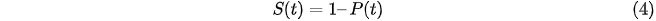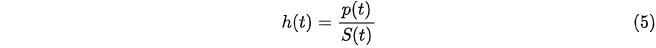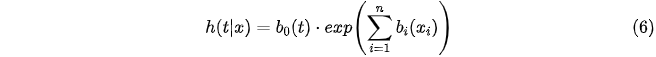This technique is ideal for our purposes because we are studying an economic outcome that takes time to eventuate. Specifically, it enables analysis of the varying lengths of time for individuals to achieve particular labour market outcomes, such as finding a full-time and/or secure job, after the completion of tertiary studies. It is advantageous because it allows gender-based unemployment patterns to be studied temporally. In this framework, ‘survival’ refers to being unemployed and ‘failure’ refers to finding a job or some other desired labour market outcome. The time a person spends in a given state (unemployment) is referred to as a ‘spell’ and the duration of a spell is considered a random variable. For a robust analysis, we employ two complementing approaches under duration modelling: (i) a non-parametric method called the Kaplan-Meier survival method and (ii) the Cox Proportion Hazard model, which is regression based.
3.1 Kaplan-Meier survival analysis
The Kaplan-Meier (KM) duration modelling technique is a non-parametric modelling approach that enables analysis through the estimation of a survival function (Kaplan and Meier 1958). To start, we define a ‘spell’ as a length of time that a homogenous group of persons experiences a state of being such as being alive or being in remission, being single or being married, being in foster care, being in detention, being unemployed or being a welfare recipient. We define an ‘event’ as the point in time when the person exits the spell. Using data, KM provides a survival rate, which is the person’s probability of staying in the spell or surviving the spell. KM also provides a hazard rate which pertains to a person’s probability of reaching the ‘event’ and exiting the spell.
In more technical language, the KM approach involves the estimation of a survival function defined as:
which gives the probability that a spell will last until a certain time t. T is a random variable that represents spell duration, while t represents the observed/actual duration. The function in (1) is formally interpreted as the probability of survival after time t. The cumulative distribution of T is denoted by:
while:
is the probability density function. Consequently, the survival function is:
and the instantaneous probability of exiting a spell is calculated using the hazard function h(t) which is written as:
Since this study is about labour market outcomes, we default to full-time unemployment as the spell and our KM surviving function S(t) measures the probability of an individual remaining in full-time unemployment. An event is then defined as finding a full-time job, and the KM hazard rate indicates the person’s probability of exiting unemployment and finding a full-time job.1 The method allows for the estimation of a life table, and a graph, called survival curve, which are all produced for a better view of the population at risk.
3.2 Time varying covariates and Cox Proportional Hazard modelling
Survival regression analysis allows us to use the duration and the exit variables in the modelling exercises and also use additional data, such as age, gender, and wages, to serve as explanatory variables or what many also call covariates. There are several ways to implement this on data, but the most popular approach is the Cox Proportional Hazard (CPH) regression model. CPH modelling employs a distribution-free approach and calculates survival rates that only depend on the ranks of the event times, rather than on their numerical values. This means that any monotonic transformation of the event times will leave the coefficient estimates unchanged.
CPH regression modelling is similar to implementing a multiple regression analysis, with the key difference that the dependent variable is the hazard function h(t) at a given time t, rather than the conventional observed y variable. The model works such that the log-hazard of an individual subject is a linear function of their static covariates and a population-level baseline hazard function that changes over time. These covariates are estimated by partial likelihood, and as such, the approach is effectively a semi-parametric modelling exercise. The approach is semi-parametric in the sense that the baseline hazard function does not have to be specified. This allows the estimation to be fully flexible, in that a different parameter can be used for each unique survival time, while simultaneously assuming the rate ratio remains proportional throughout the follow-up period. The term ‘proportional hazards’ refers to the assumption of a constant relationship between the dependent variable and the regression coefficients. This implies that the hazard functions for any two subjects at any point in time are proportional – in other words, it assumes multiplicative effects of the covariates on the hazard function.
In this paper, the form of the Cox Proportional Hazards regression model is given as follows:
where b0(t) is the baseline hazard rate and indicates the probability of experiencing unemployment when all other covariates equal zero. The regression coefficients, bi(xi), give the proportional change that can be expected in the hazard h(t|x). A hazard ratio of 1.0 means that the covariate regressor has no effect on the hazard rate, a value less than 1.0 means that the covariate regressor reduces the hazard rate, and a value greater than 1.0 implies that the covariate regressor increases the hazard rate. Note that b0(t) is the only time-dependent component in the model. The sign of the regression coefficients, bi, also play an important role – a positive sign means that the risk of the event is higher, while a negative sign means that the risk of the event is lower. The model is estimated using maximum partial likelihood techniques.
Footnotes
[1] The terms survival and hazard appear counter-intuitive at first, and at first pass, they actually are. This comes from the fact that duration modelling has its roots in the medical field where duration spells often refer to the length of time a patient lives and survives, and the exit event is death, hence the term hazard rate for what most would consider a negative outcome. For this study, it will be helpful to bear in mind that ‘surviving’ means staying unemployed, which is a negative outcome, and that the hazard event is finding a job, which is a desirable and positive outcome.
Updated