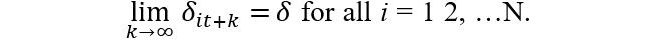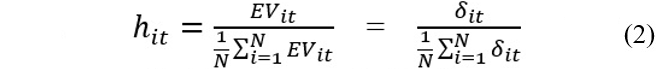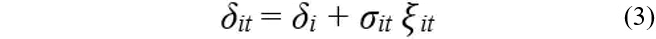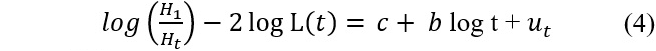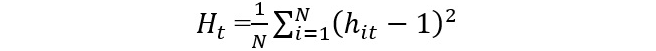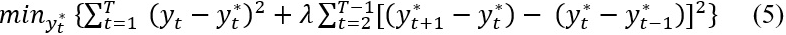3. Methodology

The advantage of using this technique lies in its ability to incorporate a nonlinear time-varying factor model in its estimation process.¹

This paper demonstrates the feasibility of applying this technique to model the transitional dynamics and long‑run behaviour of electric vehicle adoption in Australia. To facilitate this, we follow Phillips and Sul (2007) [PS hereafter] and first decompose EV adoption components into two parts as follows:

where δ_it is a time varying idiosyncratic element which measures the deviation of each region i from the common trend (µ_t).

Within this framework, the convergence to a steady state at a future date is anticipated for all N when:

The elimination of the trend component µ_t and the estimation of δ_it requires the modification of Eq. (1) such that:

where h_it is the relative measure that defines the transition path relative to the average of all regions. An econometric test of convergence can be further formulated to identify a second-round of convergence occurring between clubs. This is achieved by considering a semi-parametric form of δ_it:

where σ_it = σ_i L(t)^-1t^-α, σ_i ˃ 0, t ≥ 0, and ξ_it is an i.i.d (0,1) across i, but weakly time dependent. The function L(t) is increasing in t but diverges as t tends to infinity². From here, we set the null hypothesis of convergence as H₀: δ_i = δ, α ≥ 0, against the alternative hypothesis H_A: δ_i ≠ δ or α < 0.

The focal point of the technique is the examination of the sign of α. Even if there is a rejection of the null hypothesis of convergence in the panel, the occurrence of potential sub-convergence amongst the clubs cannot be ruled out since there is a likelihood of multiple equilibria.

In validating the null hypothesis, this club convergence technique by PS requires estimation of the following equation:

Where:

represents the square cross-sectional distance-relative transition coefficients.

For the case of b̂ = 2â, a one-sided test of b̂ ≥ 0 against the alternative hypothesis of b̂ < 0 can be constructed as the null hypothesis. At the 5 per cent level, the rejection of the null hypothesis occurs if t_b̂< -1.65³. The identification of the various clubs is achieved through the robust clustering algorithm proposed by Phillips and Sul (2007).

We now outline below the specific steps we adopted to implement this convergence club technique by PS to examine EV adoption in Australia:

1. Order the regions in the panel according to the last observation in the time series. This ranking assumes convergence is more apparent in the most recent observations. If there are significant variations within the region, the average of the last fraction of the sample can be taken to order the panel.
2. Select the first k highest regions in the panel to form subgroups G_k for some N > k > 2. After estimating regression (4) for each formed subgroup, select a core group through the following cut-off point criterion: k*=ArgMax_k[t_b̂], subject to Min_k [t_b̂] > -1.65 for k = 2, 3, …, N.
3. For the remainder regions and each of the formations, re-estimate equation (4) and add one region at a time to the core group. The inclusion of a particular region in the core group will be determined following this sign criterion [b̂ ≤ 0].
4. For the remaining regions, repeat steps 2–3 until there is no further club formation. The procedure is then terminated. When regions in the last group do not have a convergent path, then it can be concluded that they belong to a non-converging group.

As stated by PS, using the sign criterion as the decision rule in step (2) may generate an overestimated number of clubs. They recommend that it is essential to perform a club merging test in addition to estimating equation (4). We employ the Hodrick and Prescott (1997) filter to extract the trend component of the series and to generate the trend that minimises the squared changes in trend and deviations, as follows:

This filter extracts the long-run trends, while eliminating the short-run erratic behaviour of the data⁴.

Footnotes

^{[1] Recent examples include Awaworyi et al. (2018a, 2018b); Bhattacharya et al. (2020a, 2020b) and Bhattacharya and Inekwe (2021)
[2] In the PS approach, L(t) = log (t) needs to hold in order to guarantee convergence.
[3] The PS approach requires that the heteroskedastic and autocorrelation consistent standard errors for b are obtained as the ordinary least squares standard errors of the region in equation (4) may be weakly time dependent.
[4] In using the filter, the lambda is set to 10, which is approximately the recommended value for annual data.}