Our empirical strategy involves the estimation of the following basic equation form:
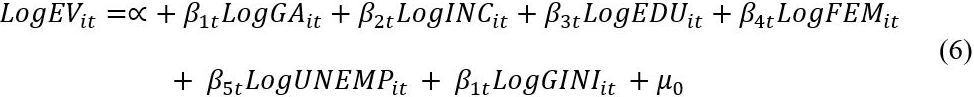
where, for any given region i and time t, EV is the ratio of registered electric vehicles to total vehicle registration, GA is green awareness measured by the number of solar installations per capita, INC is the region’s annual per capita income, EDU is the proportion of population that completed Year 12, FEM is the female-to-male ratio, UNEMP is the unemployment rate and GINI is the level of inequality. We have added these region‑level variables to the models to test whether they are also key factors influencing EV uptake in Australia, as has been found in other economies. Year‑fixed effects are included to eliminate bias from any unobserved variables that evolve over time but are constant across entities. We report our results in Table 5 below. Table 6 contains summary statistics using the modelling exercise in Section 6, and a correlation matrix of the relevant variables to facilitate discussion.
Models 1 and 2 are the models which incorporate all the hypothesised regional variables listed above. Estimation results for Model 1 shows that GA, INC and EDU all impact on EV demand significantly, while FEM, UNEMP and GINI are not significant factors. Model 2 is a modified version of Model 1, in that it includes the same regressors as in Model 1 but also includes dummy variables for the year and is a time‑fixed effects variant. Estimation results for Model 2 show that the impact of GA as a factor in EV is diminished with the addition of year dummies, but INC and EDU remain significant influences. FEM, UNEMP and GINI remain insignificant factors, as in Model 1.
Experienced analysts may observe that there is a high chance of multicollinearity within these models, which, if true, would result in less reliable coefficient estimates for β2 and β3. Multicollinearity can lead to skewed or misleading results as the high correlation between INC and EDU, for example, makes it difficult to separate individual effects on EV demand in a statistical model. Technically, multicollinearity can lead to wider confidence intervals and produce less reliable probabilities in terms of the independent variable effects. A quick inspection of the correlation matrix of the variables in the models (Table 6) reveals that INC and EDU have a strong linear relationship (ρ = 0.768). Given this, we proceed to estimate Models 3–6 by using only INC in the model (we drop EDU), along with the other variables. And as a matter of procedure, we also estimate Models 7–10 using only EDU in the model (we drop INC), along with the other variables. The results are presented in the rests of the columns in Table 5.
Model 3 shows that GA, INC and GINI are the factors that exert a significant influence on EV demand, while FEM and UNEMP are not significant. Of the significant variables, we can further say that a 10 per cent increase green awareness leads to a 2.1 per cent increase in EV registrations, all other variables remaining constant. For INC, the results indicate that a 10 per cent increase in per capita incomes is associated with an increase in EV adoption rate of about 27 per cent. For GINI, the significant negative coefficients indicates that a 10 per cent decrease in a region’s inequality level raises EV demand by 12.82 per cent or 13 per cent rounded up. Model 4 results were obtained by incorporating time-year effects in the estimation. Under this, we can see that the impact of GA on EV demand becomes insignificant, but INC and GINI remain significant factors of similar magnitudes to Model 3.
In Models 5 and 6, we continue to use INC on the right-hand side, at the expense of EDU. We also exclude UNEMP to eliminate any multicollinearity effects between INC and UNEMP. Table 6 shows that INC and UMEMP has a ρ = 0.611. Model 5 results show the significance of GA, INC and GINI, and with a similar size and impact as in Model 3. Time‑fixed effects Model 6 return results that show no significance for GA, but INC, FEM and GINI all return as highly significant factors. The size impact of INC and GINI on EV demand are similar to those we have already seen in Models 3-5. The new result here demonstrates the significance of FEM. Assuming all else constant, Model 6 reveals that an increase in the proportion of females relative to males in the region (FEM) increases EV demand by 24.34 per cent.
Table 5. Final Regression Results
| VARIABLES | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|---|
| Log GA | 0.205*** | -0.038 | 0.210*** | 0.019 | 0.208*** | 0.017 | 0.221*** | -0.053 | 0.160*** | -0.080 |
| (0.054) | (0.054) | (0.054) | (0.055) | (0.054) | (0.055) | (0.055) | (0.054) | (0.051) | (0.049) | |
| Log INC | 1.968*** | 0.791*** | 2.710*** | 2.309*** | 2.655*** | 2.369*** | ||||
| (0.309) | (0.306) | (0.230) | (0.222) | (0.181) | (0.174) | |||||
| Log EDU | 0.856*** | 1.624*** | 1.888*** | 2.054*** | 1.971*** | 2.087*** | ||||
| (0.240) | (0.233) | (0.183) | (0.164) | (0.181) | (0.162) | |||||
| Log POP | 0.129 | 0.803 | 1.258 | 2.605** | 1.346 | 2.434** | -0.778 | 0.536 | 0.586 | 1.064 |
| (1.137) | (1.045) | (1.101) | (1.047) | (1.051) | (0.997) | (1.160) | (1.044) | (1.067) | (0.951) | |
| Log EMP | 0.092 | -0.002 | 0.054 | -0.050 | -0.237* | -0.123 | -0.294** | -0.142 | ||
| (0.129) | (0.119) | (0.130) | (0.123) | (0.122) | (0.110) | (0.121) | (0.109) | |||
| Log GINI | -0.664 | -0.224 | -1.282** | -1.387** | -1.234** | -1.404** | 1.537*** | 0.586 | ||
| (0.619) | (0.569) | (0.599) | (0.563) | (0.593) | (0.558) | (0.527) | (0.478) | |||
| Constant | -34.859*** | -23.620*** | -39.680*** | -34.271*** | -38.876*** | -35.061*** | -15.663*** | -15.927*** | -16.519*** | -16.248*** |
| (3.191) | (3.123) | (2.915) | (2.818) | (2.152) | (2.085) | (1.072) | (0.964) | (1.037) | (0.928) | |
| Fixed Effects | n | y | n | y | n | y | n | y | n | y |
| Observations | 695 | 695 | 695 | 695 | 696 | 696 | 695 | 695 | 695 | 695 |
| R-squared | 0.310 | 0.427 | 0.297 | 0.386 | 0.298 | 0.386 | 0.270 | 0.421 | 0.261 | 0.420 |
| Standard errors in parentheses *** p<0.01, ** p<0.05, * p<0.1 | ||||||||||
Note: Standard errors in parentheses *** p<0.01, ** p<0.05, * p<0.1
Table 6. Summary Statistics (of variables used in Section 6 models)
| EV | GA | INC | EDU | FEM | UNEMP | GINI | |
|---|---|---|---|---|---|---|---|
| Mean | 0.00034 | 0.011 | 34114 | 48 | 1.012 | 3.1 | 0.465 |
| Median | 0.00017 | 0.010 | 31220 | 46 | 1.018 | 3.2 | 0.459 |
| Max | 0.00803 | 0.029 | 73754 | 76 | 1.070 | 6.2 | 0.610 |
| Min | 0.00001 | 0.001 | 19089 | 27 | 0.760 | 2.8 | 0.389 |
| Std Dev | 0.00064 | 0.006 | 9798 | 13 | 0.040 | 3.2 | 0.042 |
| Correlation matrix | |||||||
| EV | 1.000 | ||||||
| GA | -0.152 | 1.000 | |||||
| INC | 0.511 | -0.358 | 1.000 | ||||
| EDU | 0.495 | -0.473 | 0.768 | 1.000 | |||
| FEM | 0.123 | 0.148 | 0.090 | 0.206 | 1.000 | ||
| UNEMP | -0.286 | 0.311 | -0.611 | -0.480 | 0.251 | 1.000 | |
| GINI | 0.220 | -0.251 | 0.578 | 0.323 | 0.294 | -0.208 | 1.000 |
In Models 7–10, we use the EDU variable instead of the INC variable as a key regressor in the model. We find in Model 7 that GA, EDU and GINI are all significant factors on EV demand but note that the sign of the GINI coefficient is positive, unlike in previous models. A positive coefficient for the GINI is not as expected and is probably harder to rationalise compared to the negative coefficient found earlier. We also see in this model that UNEMP is negatively significant, albeit at the 10 per cent level only. This means that a 10 per cent decline in unemployment rates in the region can result in a 2 per cent increase in EV registrations, which is plausible. The next model Model 8, which is the time‑fixed effects version of Model 7, returns with weak results – none of the coefficients returned significant except for the coefficient of EDU. This model appears less reliable and less informative than the others we have already reviewed.
Lastly, we consider Models 9 and 10 found in the last two columns of Table 5. In Model 9, we find that GA and EDU are strongly significant factors that influence EV demand positively. In terms of size, the effect of GA appears relatively small compared to earlier models. The size impact of EDU appears close in value compared to those found in Models 7 and 8. We also see in this model that UNEMP is negatively highly significant. The coefficient value of -0.294 means that a 10 per cent decline in a regional unemployment rate results in a 2 per cent increase in EV registrations, which is also plausible. Model 10 results appear weaker compared to that of Model 9. With only one regressor showing significance, this model appears less reliable and less informative than the others already considered.
Models 5 and 6 present the most plausible model of all: green awareness, income, female population and inequality are found to influence EV adoption rates across the board. In Model 5, we find that a 10 per cent increase in green awareness results in a 2 per cent increase in EV registrations, all else being constant. Similarly, a 10 per cent increase in per capita income results in a significant increase in EV registrations of around 24–26 per cent. A 10 per cent decrease in inequality levels within a region is also found to raise EV demand by between 12–14 per cent. Finally, a 10 per cent increase in the number of females in the region relative to males raises EV demand by about 24 per cent.
Updated

